Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Potentiel électrostatique

Posté par
kamikaz 12-11-21 à 23:04

Bonsoir,

Merci d'avance.

Deux charges ponctuelles -q et 3q (avec q>0) sont placées respectivement en deux points de l'axe Ox : A(-a ; 0) et B(3a ; 0).

On considère le point M (x ; y) comme illustré sur la figure suivante :

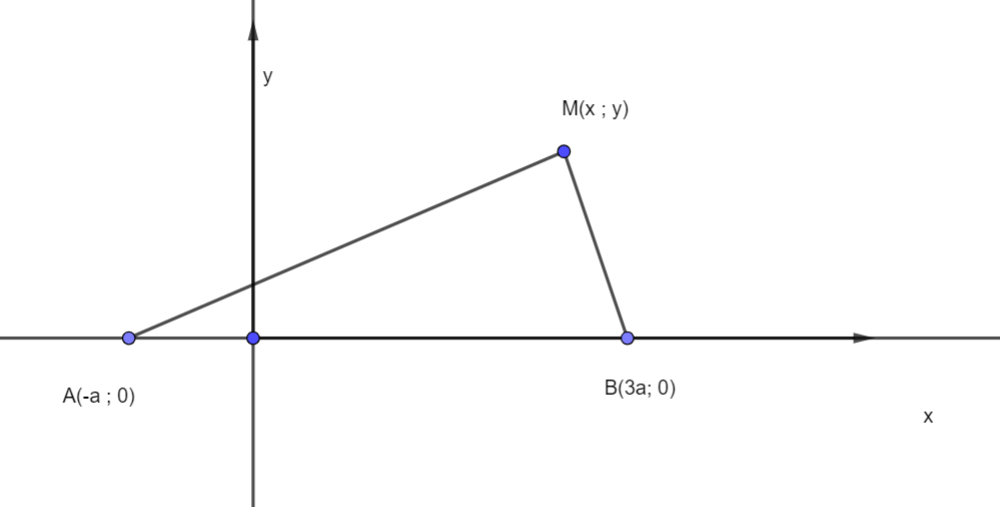
Potentiel électrostatique

1) Quelle est l'expression du champ électrostatique créé par les deux charges au point M(x ; y) ?

2) Calculer le potentiel électrostatique V(M)

3) Déterminer la nature de la courbe associée à l'équipotentielle (V =0)

Posté par
vanoisere : Potentiel électrostatique 13-11-21 à 00:43

Bonsoir
Il s'agit d'une application directe du cours. Que proposes-tu ?

Posté par
kamikazre : Potentiel électrostatique 13-11-21 à 08:51

Je n'arrive pas à retrouver le plan d'antisymétrie..

Posté par
vanoisere : Potentiel électrostatique 13-11-21 à 11:04

Avec une source constituée des charge -q et 3q, il n'y a pas de plan d'antisymétrie. Il faut juste appliquer le principe de superposition pour obtenir le vecteur champ et le potentiel V en M.

Posté par
kamikazre : Potentiel électrostatique 13-11-21 à 11:38

ok, j'ai cru qu'on devrait faire intervenir le milieu du segment [AB].

1) \vec{E}=\dfrac{-q}{4\pi \epsilon_0 r_1²}\vec{u_1} +\dfrac{3q}{4\pi \epsilon_0 r_2²}\vec{u_2} avec r1=AM et r2=BM

\vec{E}=\dfrac{-q}{4\pi \epsilon_0 [(x+a)²+y²]}\vec{u_1} +\dfrac{3q}{4\pi \epsilon_0 [(x-3a)²+y²]}\vec{u_2}

Posté par
vanoisere : Potentiel électrostatique 13-11-21 à 12:35

Oui mais je pense qu'il faut exprimer le vecteur champ dans la base (,) définissant le repère cartésien. Cela peut se faire très facilement en écrivant le vecteur champ sous la forme suivante :

\overrightarrow{E_{(M)}}=\dfrac{-q}{4\pi.\varepsilon_{o}}\cdot\dfrac{\overrightarrow{AM}}{\Vert\overrightarrow{AM}\Vert^{3}}+\dfrac{3q}{4\pi.\varepsilon_{o}}\cdot\dfrac{\overrightarrow{BM}}{\Vert\overrightarrow{BM}\Vert^{3}}=\dfrac{q}{4\pi.\varepsilon_{o}}\cdot\left[-\dfrac{\overrightarrow{AM}}{\Vert\overrightarrow{AM}\Vert^{3}}+\dfrac{3\overrightarrow{BM}}{\Vert\overrightarrow{BM}\Vert^{3}}\right]

Posté par
kamikazre : Potentiel électrostatique 13-11-21 à 13:02

D'accord, et la 2e question ?

Posté par
vanoisere : Potentiel électrostatique 13-11-21 à 13:47

Pour le vecteur E : je t'ai indiqué une méthode possible mais le calcul n'est pas achevé. Il faut exprimer les vecteur AM et BM dans la base (,) en fonction de x, y et a.
Pour le potentiel : le plus simple ici me semble-t-il, consiste à partir de l'expression du potentiel créé par une charge ponctuelle puis à appliquer le principe de superposition.

Posté par
kamikazre : Potentiel électrostatique 13-11-21 à 15:07

Ok

\vec{E}=\dfrac{q}{4\pi \epsilon_0} \left[\dfrac{\vec{MA}}{[(x+a)²+y²]^3} + \dfrac{3\vec{BM}}{[(x-3a)²+y²]^3} \right]

Citation :
Pour le potentiel : le plus simple ici me semble-t-il, consiste à partir de l'expression du potentiel créé par une charge ponctuelle puis à appliquer le principe de superposition.


J'ai pas compris

Posté par
vanoisere : Potentiel électrostatique 13-11-21 à 15:21

Cette expression du vecteur champ n'est pas fausse mais ne correspond sans doute pas à ce qui est demandé. Il faut en plus exprimer les vecteurs \vec{MA} et \vec{MB} en fonction de x, y, a , et .

Posté par
kamikazre : Potentiel électrostatique 13-11-21 à 16:38

*\vec{AM}= AM_{x} \vec{i} + AM _{y} \vec{j}

AMx=x-(-a) = x+a et AMy= y-0 = y

\vec{AM}= (x+a) \vec{i} + y \vec{j}

*\vec{BM}= BM_{x} \vec{i} + BM _{y} \vec{j}

BMx=x-3a  et BMy= y-0 = y

\vec{BM}=(x-3a)_{x} \vec{i} + y \vec{j}

Mais je pense que là çà devient vraiment compliqué parce qu'on aura : \vec{E}=\dfrac{q}{4\pi \epsilon_0} \left[\dfrac{ (x+a) \vec{i} + y \vec{j}}{[(x+a)²+y²]^3} + \dfrac{3\left[(x-3a) \vec{i}\right] + y\vec{j}}{[(x-3a)²+y²]^3} \right]

Posté par
kamikazre : Potentiel électrostatique 13-11-21 à 16:39

\vec{E}=\dfrac{q}{4\pi \epsilon_0} \left[\dfrac{ (x+a) \vec{i} + y \vec{j}}{[(x+a)²+y²]^3} + \dfrac{3\left[(x-3a) \vec{i} + y\vec{j}\right]}{[(x-3a)²+y²]^3} \right]

Posté par
vanoisere : Potentiel électrostatique 13-11-21 à 18:23

La méthode est bonne. Juste une étourderie de signe : tu as remplacé  
\overrightarrow{MA} par \overrightarrow{AM}.

Posté par
kamikazre : Potentiel électrostatique 13-11-21 à 18:36

Ah oui ; \vec{E}=\dfrac{q}{4\pi \epsilon_0} \left[-\dfrac{ (x+a) \vec{i} + y \vec{j}}{[(x+a)²+y²]^3} + \dfrac{3\left[(x-3a) \vec{i} + y\vec{j}\right]}{[(x-3a)²+y²]^3} \right]

Posté par
vanoisere : Potentiel électrostatique 13-11-21 à 18:55

C'est bien cela ; il y a bien peu de simplifications possibles ; les simplifications auraient été plus nombreuses en imaginant la charge 3q en A et la charge -q en B...

Posté par
kamikazre : Potentiel électrostatique 13-11-21 à 19:06

Est ce qu'on ne devrait pas utiliser le milieu du segment [AM] ?

Posté par
vanoisere : Potentiel électrostatique 13-11-21 à 19:39

Pourquoi  ?
N'oublie pas que le point M est quelconque dans le plan.  Le milieu du segment AM ne joue pas de rôle particulier.

Posté par
kamikazre : Potentiel électrostatique 14-11-21 à 18:13

Ah ok même si cela me paraissait logique..

Du coup comment intégrer cette expression pour trouver le potentiel V(M) au point M ?

Posté par
vanoisere : Potentiel électrostatique 14-11-21 à 18:29

L'expression du vecteur champ étant relativement compliquée, obtenir V à partir du vecteur champ en utilisant la relation \overrightarrow{E}=-\overrightarrow{grad}\left(V\right) est assez compliqué. Comme déjà écrit, il me semble préférable de partir de l'expression du potentiel créé par une charge ponctuelle puis d'utiliser le principe de superposition.

V_{(M)}=\dfrac{-q}{4\pi.\varepsilon_{o}.\Vert\overrightarrow{AM}\Vert}+\dfrac{3q}{4\pi.\varepsilon_{o}.\Vert\overrightarrow{BM}\Vert}

Reste à exprimer V(M) en faisant intervenir les coordonnées x et y de M.

Posté par
kamikazre : Potentiel électrostatique 14-11-21 à 19:04

Comment çà ?

E_{A/M}=\dfrac{-q}{4\pi.\varepsilon_{o}.\Vert\overrightarrow{AM}\Vert} et E_{B/M}=\dfrac{3q}{4\pi.\varepsilon_{o}.\Vert\overrightarrow{BM}\Vert} non ?

Pourquoi est ce que V(M) =E_{A/M}+E_{B/M} ?

Posté par
kamikazre : Potentiel électrostatique 14-11-21 à 19:05

Ah oui désolé j'avais mal vu..

Posté par
vanoisere : Potentiel électrostatique 14-11-21 à 19:23

Citation :
E_{A/M}=\dfrac{-q}{4\pi.\varepsilon_{o}.\Vert\overrightarrow{AM}\Vert} et E_{B/M}=\dfrac{3q}{4\pi.\varepsilon_{o}.\Vert\overrightarrow{BM}\Vert} non ?

Je n'y crois pas... Tu ne vas tout de même pas me dire qu'après tous ces exercices d'électrostatique, tu en es encore à confondre vecteur champ et potentiel...

Posté par
kamikazre : Potentiel électrostatique 14-11-21 à 20:00

kamikaz @ 14-11-2021 à 19:05

Ah oui désolé j'avais mal vu..

Posté par
kamikazre : Potentiel électrostatique 15-11-21 à 00:33

V_{(M)}=\dfrac{-q}{4\pi.\varepsilon_{o}.[(x+a)²+y²]}+\dfrac{3q}{4\pi.\varepsilon_{o}.[(x-3a)²+y²]}

3) V_{(M)}=0 \iff \dfrac{q}{4\pi.\varepsilon_{o}.[(x+a)²+y²]}=\dfrac{3q}{4\pi.\varepsilon_{o}.[(x-3a)²+y²]}  \iff \dfrac{1}{(x+a)²+y²}=\dfrac{3}{(x-3a)²+y²} \iff (x-3a)²+y²=3[(x+a)²+y²] \iff 2x(x+6a)-6a²+2y²=0 qui est l'équation d'un cercle.

Donc la courbe associée à l'équipotentielle (V =0) est un cercle.

En utilisant le milieu du segment [AB] ; on trouve une droite.

Or une droite est un cercle de rayon infinie et ici on a bien un cercle de rayon infinie lorsque a est de plus en plus grand..

Posté par
vanoisere : Potentiel électrostatique 15-11-21 à 12:40

Tu as oublié les racines carrées dans l'expression du potentiel mais cela n'impacte pas la suite.
Je pense qu'il faut ensuite trouver les coordonnées du centre du cercle et son rayon. Cela revient à écrire l'équation sous la forme :
(x-xc)2+(y-yc)2=R2

Citation :
En utilisant le milieu du segment [AB] ; on trouve une droite.

Cette phrase est pour moi incompréhensible...

Posté par
kamikazre : Potentiel électrostatique 15-11-21 à 16:02

L'équation de ce cercle est : [x-(-3a)]²+y²=(\sqrt{12}a)²

Donc il s'agit du cercle de centre P(-3a ; 0) et de rayon \sqrt{12}a

Posté par
vanoisere : Potentiel électrostatique 16-11-21 à 11:33

D'accord avec toi !
PS :

\sqrt{12}=2\sqrt{3}

Posté par
kamikazre : Potentiel électrostatique 16-11-21 à 17:27

Ok, merci beaucoup.

J'ai un examen d'électrostat demain qu'est ce que vous pouvez me conseiller s'il vous plaît

Posté par
vanoisere : Potentiel électrostatique 16-11-21 à 17:32

Si tu as parfaitement compris toutes les résolutions d'exercices traitées sur ce forum, cela devrait aller !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !