Bonjour, je ne sais pas si l'erreur vient de moi ou de la correction du manuel :

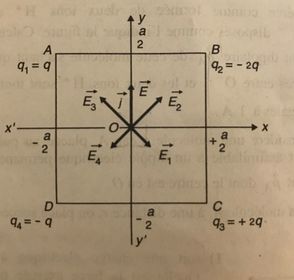
Dans un exercice en 2 parties, je dois trouver le champs en O (= centre de mon carrée).

J'ai calculé le champs, (jusqu'ici c'est en accord avec la correction) :


( Le champ est dirigé suivant l'axe y'oy
   dans le sens positif de l'axe)

Ensuite je dois déterminer le potentiel. C'est là que je ne trouve pas le même résultat.

En partant du sommet haut gauche du carré, dans le sens horaire j'ai q1 = q ; q2 = -2q ; q3 = + 2q ; q4 = - q.

Le potentiel est, selon moi :



Seulement, dans la correction le
est au dénominateur, donc comme suit :



Bon, finalement ça donne le même résultat, mais j'aimerais savoir pourquoi on met au dénominateur.

Cordialement