Inscription / Connexion Nouveau Sujet
Potentiel des actions extérieures
Bonsoir,
Je me trouve devant un système dont j'ai du mal à déterminer l'énergie potentielle.
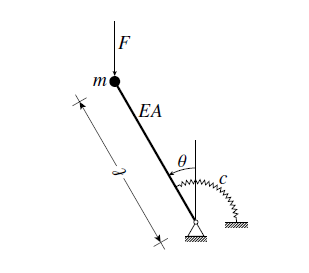
La barre peut se déformer dans le sens longitudinal (les déformations de flexion étant négligées)
J'ai déterminé l'énergie potentielle de déformation, égale à
où E est le module d'Young, A la section droite de la barre, l sa longueur, c la raideur en torsion du ressort en pied (couple de rappel égal à
. Mais quid du potentiel des forces extérieures ?
Je sais qu'il est égal à Fu, où u est le déplacement vertical du point d'application de la force F (déplacement dans le sens de la force), mais comment le relier à theta et epsilon ?
Merci beaucoup pour votre aide !
Bonjour
Par analogie avec l'énergie potentielle de pesanteur, il est facile de montrer que l'énergie potentielle associée à une force verticale descendante d'intensité F fixe est égale au produit de F par l'altitude. Le niveau d'altitude nulle peut être choisi arbitrairement puisque seules les variations d'énergie potentielle ont un sens physique. Pour F, on peut donc poser :
Ep=F.u=F.l.cos( )
)
Je ne suis pas spécialiste de RDM mais la présentation du problème m'étonne.
1 : avec une simple tige de poids négligeable et une force F constamment verticale et non colinéaire à la tige, il ne me semble pas réaliste de négliger la flexion devant la compression.
2 : provoquer une diminution de longueur non négligeable de la tige dans ces conditions supposerait un ressort spiral extrêmement raide...
3: le schéma fait apparaître une surcharge de masse m à l'extrémité supérieure de la tige. Et si F désignait simplement le poids de cette surcharge ?
4 : dans ce cas, négliger les déformations de la tige ramène à l'étude d'un simple métronome sans intervention de la RDM...
Tout cela sous réserve bien sûr : sans énoncé complet du problème...


