Inscription / Connexion Nouveau Sujet
position de centre de gravité d'une pile
bonjour tout le monde,
Pourriez vous me corriger la réponse .
Je vous remercie d'avance pour votre aide précieuse..
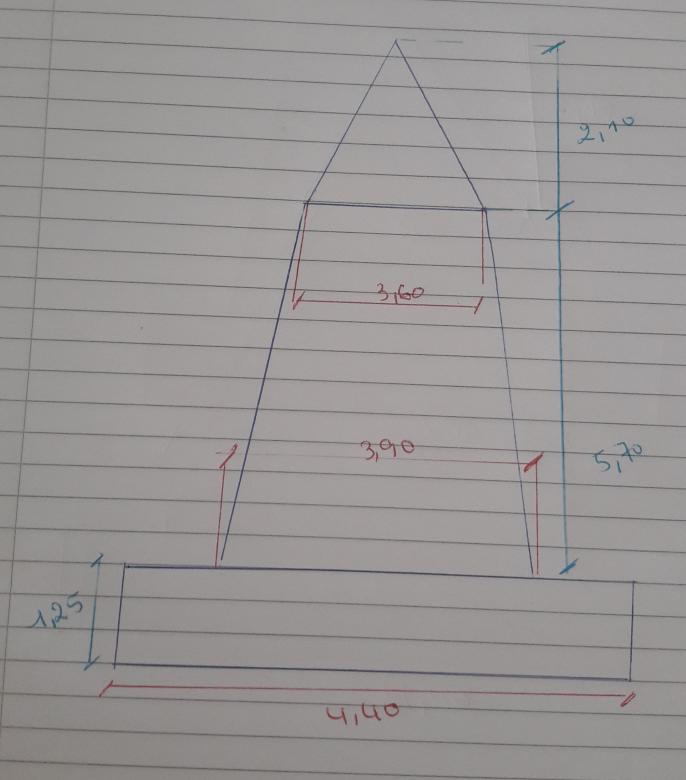
Déterminer la position du centre de gravité de la pile de la surface plane dont la section est représentée sur le schéma ci-joint
La réponse:
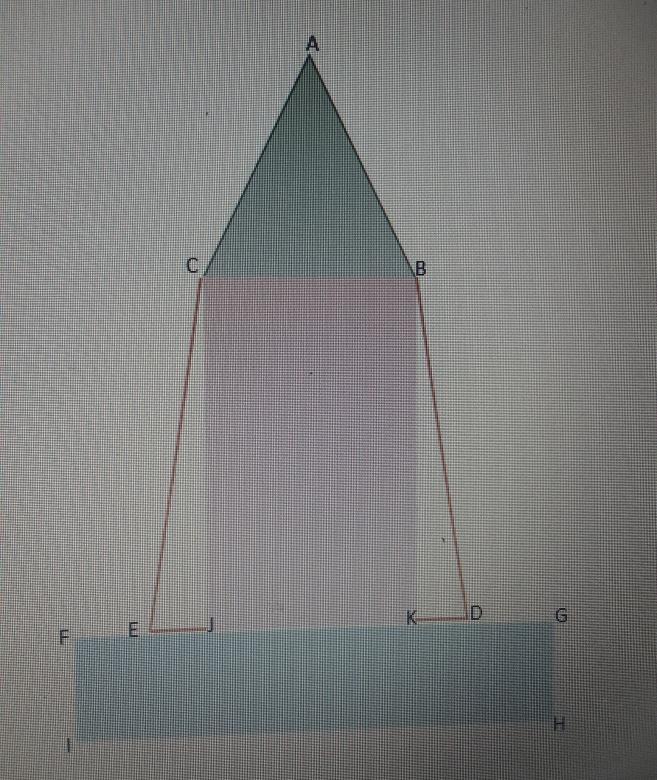
Pour trouver la position du centre de gravité de la pile j'ai décomposé celle-ci à des surfaces partielles, en ce qui concerne le trapèze intermédiaire je considère qu'il est constitué d'un rectangle est deux demi-triangles (voir schème ci-joint).
• un triangle isocèle ABC
• Un rectangle CBKJ
• 2 demi triangles
• Un rectangle FGHI
Et j'ai additionner les moments statiques des toutes les surfaces.
Le moment statique d'une section S par rapport à l'axe Ox se définit comme
Sx=∭_s▒ydxdy
De même, par rapport à l'axe Oy :
Sy=∭_s▒xdxdy
On montre que le moment statique SΔ d'une section de densité homogène, par rapport à un axe Δ, est égal au produit de l'aire A de cette section par la distance d de son centre de gravité CG à l'axe.
SΔ= d (CG, Δ). A
ELEMENTS Dim. Aire CG Le moment St
Rectangle FGHI 1.25 X 4.40 A= 4.40 x 1.25=5.50 CG2 =h/2 SΔ= d (CG, Δ). A
SΔ= (h )/2 x A
SΔ= (1.25 )/2 x 5.50= 3.43
Rectangle CBJK 3.60 X 5.70 A= 3.60 X 5.70= 20.52 CG2 =h/2 SΔ= d (CG, Δ). A
SΔ= (h )/2 x A
SΔ= (5.70 )/2 x 20.52 = 58.42
Triangle isocèle h= 2.10 A=base x h/ 2 CG= h/3 SΔ= d (CG, Δ). A
base =3.60 A= (3.6*2.1)/2= 3.78 CG= 2.1/3=0.7 SΔ= (h )/3 x A
SΔ= 2.10/3 x 3.78
SΔ = 2.65
Demi triangle1 h= 5.70 A=base x hauteur / 2 CG= h/3
base = (3.90-3.60) /2 =0.15 A= (5.70*0.15)/2= 0.43 CG= 5.70/3=1.9
SΔ= d (CG, Δ). A
SΔ= (h )/3 x A
SΔ= 5.70/3 x 0.43
SΔ = 0.81
Demi triangle2 h= 5.70 A=base x hauteur / 2
base = (3.90-3.60) /2 =0.15 A= (5.70*0.15)/2= 0.43 CG= h/3
CG= 5.70/3=1.9
SΔ= d (CG, Δ). A
SΔ= (h )/3 x A
SΔ= 5.70/3 x 0.43
SΔ = 0.81
XG=(A1*XG1 + A2*XG2+ A3*XG3+ A4*XG4 + A5*XG5)/(A1+A2+A3+A4+A5)
XG= (3.43+ 58.42+ 2.65+ 0.81 + 0.81)/(5.50+20.52+3.78+0.43+0.43) = 2.16
Bonjour ,
Je ne comprends pas bien votre énoncé :
" la pile de la surface plate " ???
Si ce sont des surfaces , je vois seulement 3 surfaces avec chacune leur CG et leur "poids " propre . Un rectangle , un trapèze , un triangle : pourquoi faire plus compliqué ?
Déjà , c'est symétrique , le CG résultant est sur l'axe
Pour un trapèze isocèle de grande base B, de petite base b et de hauteur h la position du centre de gravité G comptée à partir du milieu O de sa grande base est donnée par :
Si cela peut vous aider , je trouve le CG résultant à + 3.88 par rapport au trait de base le plus inférieur : cela paraît possible , j'espère ne pas avoir fait d'erreur .
bonjour ,
merci à tous pour vos réponse......vous avez tout à fait raison.
Etant donné que la section est symétrique, le centre de gravité se trouve sur son axe de symétrie.
..Donc avec:
Rectangle FGHI
SΔ= (h )/2 x A
SΔ= (1.25 )/2 x 5.50 SΔ= 3.43
trapèze
SΔ= ( (B+2b)/(B+b)+H/3 ) x A
SΔ= 2.81x 21.38 SΔ= 60
Triangle isocèle
SΔ= (h )/3 x A
SΔ= 2.10/3 x 3.78
SΔ = 2.65
On aura
XG=(A1*XG1 + A2*XG2+ A3*XG3)/(A1+A2+A3)= +2.16
je vous prie de bien vouloir me montrer comment avez-vous obtenu le résultat 3.89.
Merci
Je ne reconnais aucune valeur attendue .
Quelle est la valeur des 3 surfaces ?
En prenant le trait du rectangle le plus bas comme origine , quelle est l'altitude des 3 CG ?
La surface du rectangle est 5.5 ( unité arbitraire , car on ne sait pas si ce sont des mètres...)
L'altitude de son CG est à 0.625 unité arbitraire .
J'ai l'impression que vous n' avez pas bien vu comment se calcule le CG résultant .
Bonsoir,
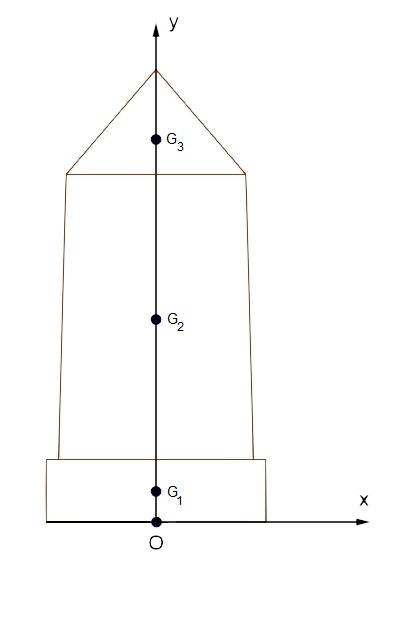
Trouver le centre de gravité G de cet ensemble revient à trouver le barycentre des points G1, G2, G3 centres de gravité du rectangle, du trapèze et du triangle affectés des aires correspondantes.
Par projection sur l'axe Oy on obtient :
On a
Bonsoir,
La position des centres de gravité de chaque partie doit être calculée à partir de la même origine.
Ton calcul est donc bon pour le rectangle, mais il faut le revoir pour le trapèze et pour le triangle.


