Inscription / Connexion Nouveau Sujet
Polarisation par une lame demi onde.
Bonjour,
On me demande de démontrer qu'une lame demi onde provoque la rotation d'une polarisation rectiligne d'un angle , si
est l'angle entre la direction de polarisation et l'axe rapide de la lame.
Je choisis donc pour cela une lame demi onde d'axe rapide Y, qui forme donc un angle avec l'axe y du labo qui sera aussi l'axe sur lequel mon rayon sera polarisé (comme demandé dans l'énoncé).
J'ai donc la matrice qui après rotation par
(pour la projeté dans le référentiel du labo) donne
J'applique donc cette matrice à mon vecteur de polarisation d'entrée pour avoir la polarisation de sortie :
Soit
Voici donc mon résultat, cependant il ne s'agit pas d'une rotation de par rapport à l'axe de polarisation d'entrée comme demandé dans l'énoncé...
De plus j'ai remarqué que si je faisais le même raisonnement avec l'axe rapide de la lame en Y mais la polarisation selon x (ref du labo) j'obtenais soit cette fois une rotation comme demandé dans l'énoncé mais avec l'angle
formé avec l'axe lent de la lame. Quelqu'un pourrait t'il m'éclairer sur mon erreur ? Peut être que je confond l'axe lent et l'axe rapide ? ou que j'interprète mal l'énoncé.
Merci d'avance, bonne journée.
Je me suis trompé dans l'écriture de dans le post précedent
Bonjour,
On me demande de démontrer qu'une lame demi onde provoque la rotation d'une polarisation rectiligne d'un angle
Je choisis donc pour cela une lame demi onde d'axe rapide Y, qui forme donc un angle
J'ai donc la matrice
J'applique donc cette matrice à mon vecteur de polarisation d'entrée pour avoir la polarisation de sortie :
Soit
Voici donc mon résultat, cependant il ne s'agit pas d'une rotation de
De plus j'ai remarqué que si je faisais le même raisonnement avec l'axe rapide de la lame en Y mais la polarisation selon x (ref du labo) j'obtenais
Merci d'avance, bonne journée.
je trouve
Bonjour
Je ne suis pas bien familiarisé avec le formalisme que tu utilises...
Ce que je sais : une lame demie-onde transforme une onde polarisée rectilignement en une onde transmise polarisée rectilignement, la direction de polarisation de l'onde transmise étant la direction symétrique de celle de polarisation de l'onde incidente par rapport à l'axe rapide. Si tu notes  l'angle entre la direction de polarisation de l'onde incidente et la direction de l'axe rapide, la direction de polarisation subit bien une déviation de 2
l'angle entre la direction de polarisation de l'onde incidente et la direction de l'axe rapide, la direction de polarisation subit bien une déviation de 2 .
.
Quelques schémas et quelques explications ici :
![]()
Bonsoir,
j'utilise le formalisme de Jones, c'est à dire que pour une lame demi onde on a :
pour un axe rapide selon Y.
Et donc on peut aussi écrire pour simplifier :
donc si on néglige la constante (inutile vu que l'on souhaite simplement avoir la polarisation) on a :
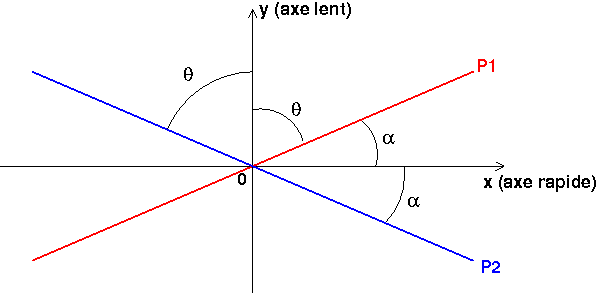
Cependant je ne comprend pas comment aborder le problème, en effet je considère avec l'image ci jointe que {x0,y0} est le référentiel du labo tandis que {x1,y1} est celui de la lame. Pourquoi lorsque l'on me dit de démontrer que la polarisation est tourné de cela ne marche pas si l'axe rapide est x1 et la polarisation selon x0 alors que l'énoncé semble dire cela ? De plus pourquoi cela marche si on considère que y1 est l'axe rapide avec la polarisation toujours selon x0 (alors que dans ce cas
 est donc formé entre l'axe lent et la direction de polarisation..) ?
est donc formé entre l'axe lent et la direction de polarisation..) ?
Merci d'avance de votre aide!
Je te fournis une démonstration physique, pour le reste, je te laisse te débrouiller avec tes matrices mais je pense que ce que tu as obtenu au début est en fait correct... Je m'explique.
Je suppose la direction de polarisation incliné de  par rapport à l'axe rapide et donc de son complémentaire
par rapport à l'axe rapide et donc de son complémentaire  par rapport à l'axe lent. En imaginant une onde incidente plane monochromatique sous incidente normale polarisée rectilignement suivant la direction (P1). Le vecteur champ électrique associé à l'onde au niveau de la face d'entrée a pour composantes :
par rapport à l'axe lent. En imaginant une onde incidente plane monochromatique sous incidente normale polarisée rectilignement suivant la direction (P1). Le vecteur champ électrique associé à l'onde au niveau de la face d'entrée a pour composantes :
En notant e l'épaisseur de la lame, nx et ny les indices de réfractions, le vecteur champ à la sortie de la lame a pour expression :
Pour une lame demie-onde :
La direction de polarisation (P2) est donc la symétrique de (P1) par rapport à l'axe rapide mais c'est aussi la symétrique de (P1) par rapport à l'axe lent. En d'autre terme : si tu notes  l'angle entre la direction de (P1) et l'axe rapide, tu peux considérer que la direction de polarisation tourne de 2
l'angle entre la direction de (P1) et l'axe rapide, tu peux considérer que la direction de polarisation tourne de 2 ; si tu notes
; si tu notes  l'angle entre (P1) et l'axe lent; tu peux aussi considérer que la direction de polarisation a tourné de l'angle 2
l'angle entre (P1) et l'axe lent; tu peux aussi considérer que la direction de polarisation a tourné de l'angle 2 ... Mathématiquement cela s'explique par le fait qu'une avance de phase de
... Mathématiquement cela s'explique par le fait qu'une avance de phase de  radians est équivalent à un retard de phase de
radians est équivalent à un retard de phase de  rad : cos(x+
rad : cos(x+ )=cos(x-
)=cos(x- )...
)...
Attention : cela ne sera pas vrai pour les lames quart onde car cos(x+ /2)
/2) cos(x-
cos(x- /2) dans le cas général. Il est donc préférable de raisonner toujours à partir du même axe : en général l'axe rapide ...
/2) dans le cas général. Il est donc préférable de raisonner toujours à partir du même axe : en général l'axe rapide ...