En fait c'est bizarre ce que je viens d'écrire (il me semble). Bon en fait ce doit être la vitesse qui périodique parce que la trajectoire on l'a déjà ! Par contre comment faire pour avoir l'expression de la vitesse?

Il s'agit de montrer que le point pesant, lâché en un point quelconque de la piste cycloïdale, y revient au bout d'un temps constant.
Cela peut se faire en déterminant l'abscisse curviligne  s  de la cycloïde en fonction du paramètre  u , puis en calculant l'énergie mécanique du point pesant en fonction de l'abscisse curviligne.

Merci en fait c'était pas si terrible que ça, j'aurais du mieux lire l'énoncé
En tout cas merci !

L'énoncé n'est pas clair.

Certes, si un point matériel est laché sans vitesse initiale sur la cycloïde donnée en équation, il va osciller indéfiniment dans une seule et même "boucle" de la cycloïde.

MAIS, s'il est lancé à une vitesse initiale suffisante, alors le point matériel va passer d'une boucle à l'autre de la cycloïde et ce mouvement ne sera alors pas périodique dans l'espace (puisqu'il continuera vers x --> oo), reste encore à voir comment le point matériel est rendu solidaire de la cycloïde pour passer les loopings.

Et comme il n'y a aucune indication sur la vitesse initiale ... on peut faire ce qu'on veut.
-----

En éliminant le paramètre t (qui n'a rien à voir acec le temps) entre les 2 équations données, on peux trouver y = f(x) ...

Voila par exemple ce que cela donne avec b = 2



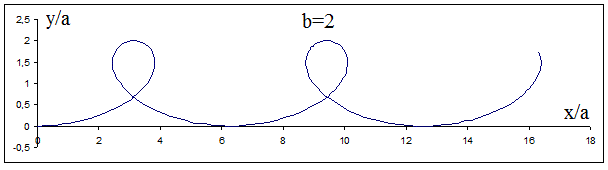
C'est la représention (dans l'espace) de la cycloïde.
-----
Sauf distraction.