Inscription / Connexion Nouveau Sujet
Plaque posée dans un angle avec frottement
Bonjour,
Voici une question que je me pose par intérêt personnel.
Voici, ci dessous une plaque (AB en bleu) posée sur deux murs (en rouge) vue de profil. On considère que la plaque est homogène et donc son centre de gravité se trouve en G milieu de AB.
Je voudrais calculer les forces en A et B.
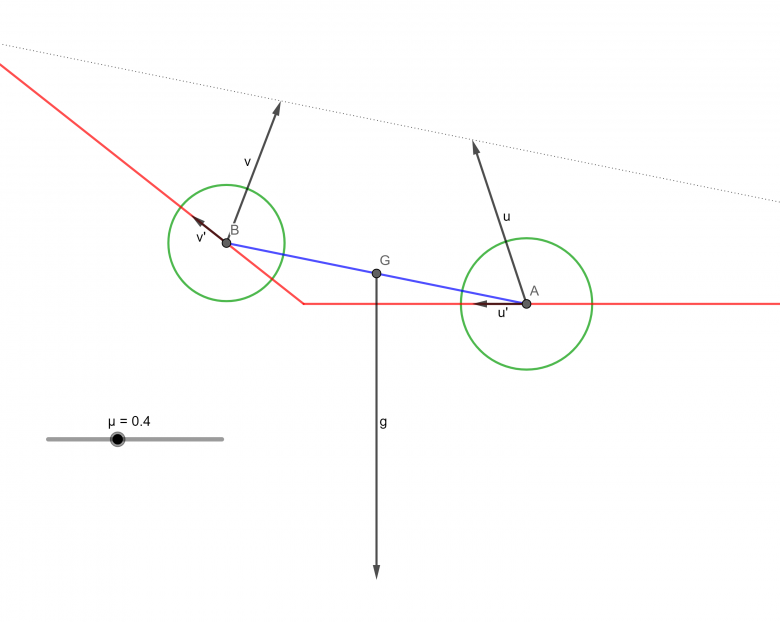
S'il n'y avait pas de frottement, la plaque glisserait. Mais en présence de frottement, je trouve une infinité de solutions possibles.
Parl'équilibre des moments, la composante de u perpendiculaire à la plaque doit être égale à la moitié de celle du poids de la plaque (g). Pareil pour v. C'est la ligne en pointillés.
Par contre la composante parallèle à la plaque peut prendre n'importe quelle valeur du moment que les composantes parallèles aux murs soient inférieur aux forces de friction (dont les limites sont représentées en vert).
On a aussi par l'équilibre des forces que u+v+g=0.
Il me une liberté. Est-ce qu'il me manque une contrainte? Comment déterminer la valeur (unique) qu'il y aura en réalité?
J'ai essayé de minimiser "l'énergie du système" en posant u=v = -g/2. Mais dans ce cas v' est trop grand et la plaque glisserait en B, reportant une partie de la force en A.
La réponse serait-elle que v' est juste sur le cercle? Celà Minimiserait l'énergie avec la contrainte de ne glisser ni en B ni en A. Je ne sais pas si ça a du sens 
Merci 
Bonjour,
Il ne me me parait pas anormal qu'il y ait une infinité de de solutions : imaginer une échelle que vous posez contre un mur : il n'y a pas une seule solution possible.
La force appliquée sur le mur par cette échelle doit bien avoir une valeur définie. Non?
On connait la position de la plaque et des murs. On sait que la plaque est statique (pas de glissement). On connait le coefficient de frottement entre la plaque et les murs. On connait le poids de la plaque et son centre d'inertie.
On cherche les forces aux points de contact entre la plaque et les murs.
Je vois ici une autre contrainte: ![]() .
.
Ils considèrent que les forces de frictions sont proportionnelles aux forces normales. Pas seulement les force de friction limite.
Ce qui signifie que l'angle de u et v par rapport aux murs est égal.
C'est en effet une solution qui me semble plutôt réaliste.
Qu'est-ce que vous en pensez?
Je ne voudrais pas être catégorique mais je pense que les forces dépendent de la manière donc on pose l'échelle.
En supposant qu'il y ait une solution unique, cela dépendrait de termes supplémentaires, par ex. l'élasticité de l'échelle, mais cela sort de mon domaine de compétence.
Tant qu'à la proportionnalité force tangentielle/force normale, cela signifie que l'on se place à la limite du glissement, pas vraiment une bonne idée pour une échelle.
Oui, j'ai bien l'impression qu'on a différentes solutions en fonction de comment on pose l'échelle.
Dans les cas et
ont a fait glisser l'échelle jusqu'à ce qu'elle accroche.
Dans le cas ont minimise le risque de glissement. A noter qu'on est à la limite du glissement seulement si
.
Toutes les solutions telles que et
seraient valides.
Par exemple, on pourrait comprimer l'échelle entre les deux murs de façon à augmenter les forces parallèles à l'échelle. On augmente ainsi la force totale appliquée sur chaque mur. Sans pour autant que la solution devienne invalide.
Bonjour,
Ce problème de non résolubilité est connu en mécanique, et c'est lié au fait que le "mécanisme" étudié est hyperstatique. On peut déterminer le degré d'hyperstaticité (= le nombre de paramètres statiques en trop) par une étude qualitative des liaisons.
Dans ce cas simple, on ne peut écrire qu'un seul PFS (principe fondamental de la statique) donc seulement 3 équations (système en 2D) - 2 résultantes et 1 moment.
Cependant, il y a 2 liaisons avec la bâti, chacune ayant 2 inconnues de liaison donc pouvant transmettre 2 efforts indépendants (normal, tangentiel) sous la limite dite du cône de frottement, donc on a 4 inconnues. Inutile de chercher plus loin, il y a plus d'inconnues que d'équations, et le PFS seul ne permet pas de résoudre.
La méthode rigoureuse est de tenir compte de la déformation de AB engendrée par les efforts càd de quitter le monde de la physique des solides indéformables. Pour le dire mathématiquement, on ajoute au PFS une équation qui relie une force inconnue à des paramètres géométriques du système (qui étaient supposés constants dans le monde du solide indéformable).
Se placer en limite de glissement sur l'un des contacts est aussi satisfaisant mathématiquement car on élimine ainsi une inconnue. Et du point de vue ingénierie aussi car cela donne souvent un "worst case". Mais il faut bien savoir pourquoi on le fait.
Bonjour,
On peut calculer les 2 limites entres lesquelles varient les réactions aux appuis ... pour qu'il y ait équilibre.
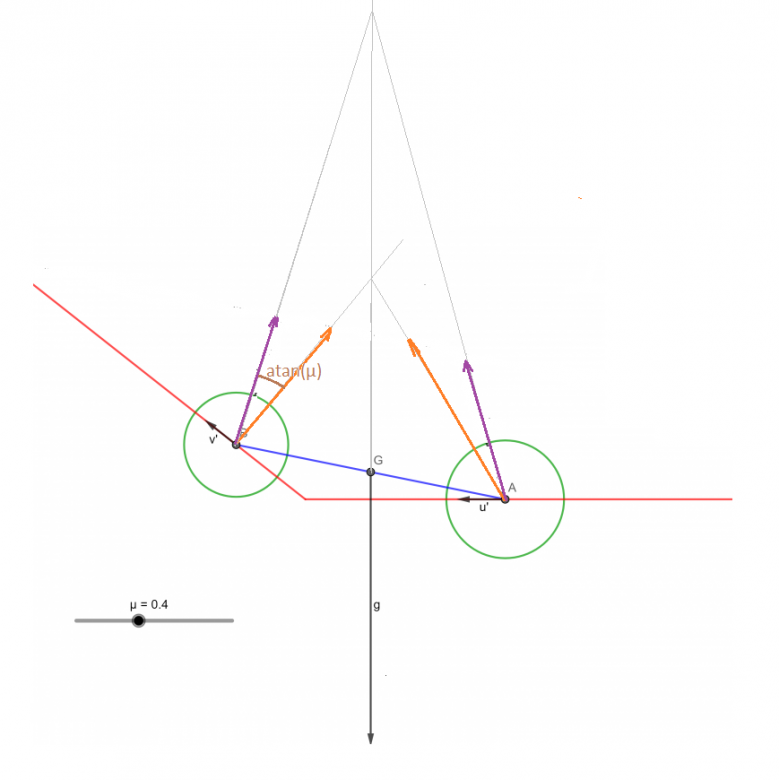
Sur le mur oblique :
Force de frottement f comprise entre 0 et son max ...
A f = 0, la direction de la force (mur oblique-échelle) est perpendiculaire au mur
A f = max, la direction de la force (mur oblique-échelle) fait un angle = atan(µ) avec la normale au mur.
On peut donc déterminer les limites entres lesquelles varient les réactions aux appuis. (entre les flèches orange et mauve sur mon dessin).