Bonjour,

La symétrie d'un système c'est avant tout le premier point de vue :
"le symétrique de cette boule par rapport à ce plan est une boule identique et de même charge" : la symétrie ne change rien au système.
Et partant de là, si le plan ne coupe pas l'objet en deux parties égales, je ne vois pas comment il pourrait y avoir symétrie.
Après, pour "voir" cette symétrie, dire qu'une demi-sphère est la symétrique de l'autre par la symétrie, pourquoi pas ? Auriez-vous des liens pour comprendre ce découpage ?
Vous faites quel découpage pour les symétries par rapport à un axe ou un point ?

Ce que je demande peut-être maladroitement, c'est de savoir si le "critère" pour dire qu'un plan est un plan de symétrie de la distribution de courant c'est que quand un on prend le symétrique de notre objet par ce plan on obtient le même objet avec la même charge/même courant.
Par exemple, pour le fil infini, on a dit dans notre cours que le plan représenté est un plan de symétrie pour le plan infini, ce que je demande, c'est : est-ce que l'on dit ça parce que quand on fait le symétrique de ce fil par le plan, on obtient la même chose, où est-ce que c'est parce que ce plan coupe le fil en deux (ce qui me paraît bizarre puisque le point étant quelconque, ce plan n'a aucune raison d'intersecter le fil en question )

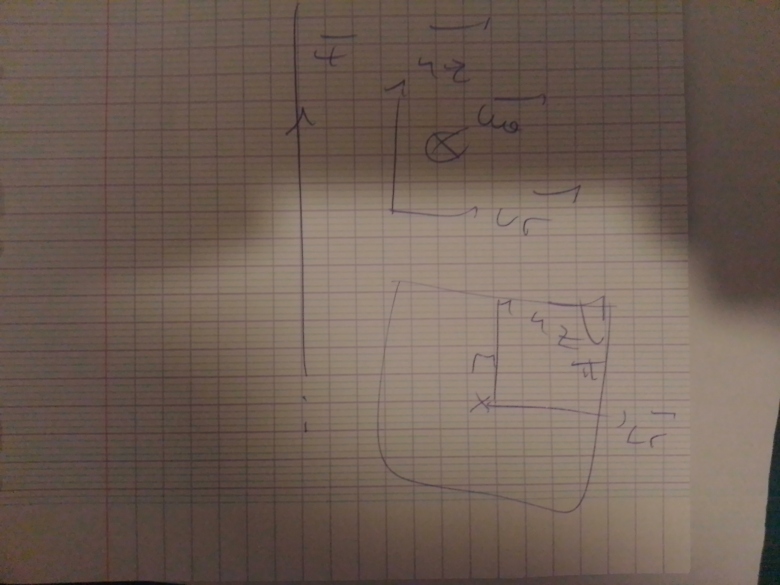
Vous avez raison : le critère est bien "un plan est un plan de symétrie de la distribution de courant si le symétrique de notre objet par ce plan est le même objet avec la même charge/même courant".
Si le plan n'intersecte pas le fil, ce plan n'est pas un plan de symétrie : le symétrique du fil est différent du fil.
Pour que "quand on fait le symétrique de ce fil par le plan, on obtient la même chose", il faut bien que le plan passe par le fil.
Le point M est quelconque, mais le plan est celui défini par M et le fil (donc le plan (M,axe z) qui passe donc obligatoirement par le fil.

Voir le dessin ci-dessous.

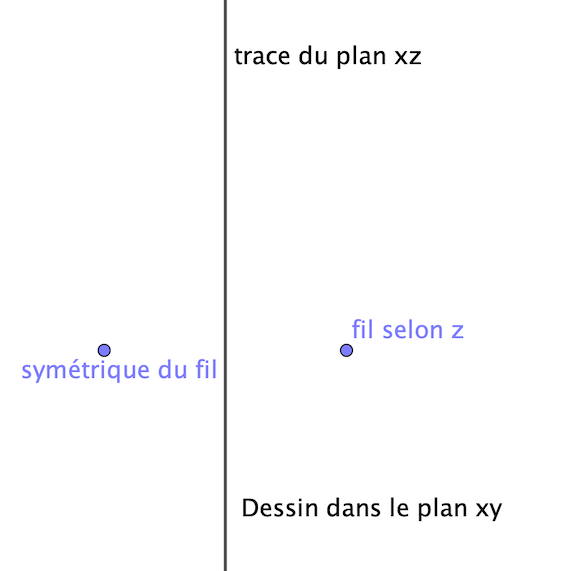
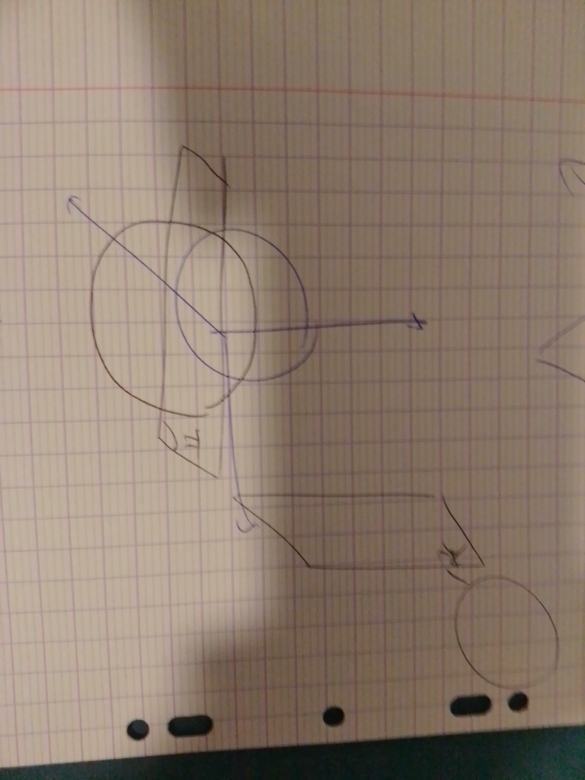
Juste pour être sûr, pour l'exemple de la boule que j'ai pris tout à l'heure, le plan que j'ai représenté en bleu est bien un plan de symétrie, puisque par passage au symétrique on obtient la même boule, alors que les deux plans que j'ai représentés en noir donnent une boule qui n'est pas confondue avec la boule représentée en bleu et donc ne sont pas des plans de symétrie.

C'est bien cela.

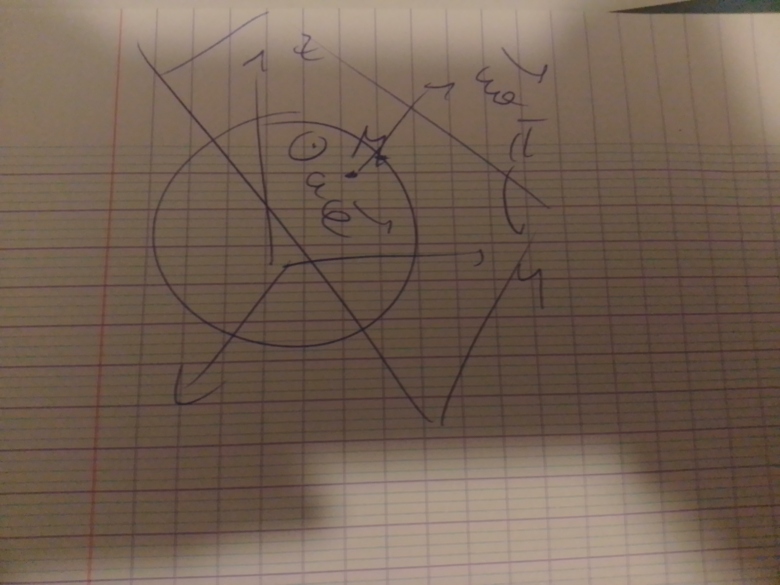
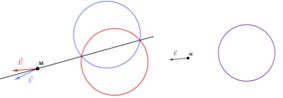
Dans le cas à droite, les deux problèmes "champ créé par M par les sphères rouges et bleues" est le même ; on peut donc en déduite des propriétés de

Dans le cas à gauche, les deux problèmes sont différents, la symétrie entre les deux cas permet juste de dire que   est symétrique de

Bonjour,
Vous voulez donc dire que à droite on est bien en présence d'un plan de symétrie physique pour l'objet alors qu'à gauche ce n'est pas le cas ?

(et cela vient bien du fait pour la cas à gauche que les deux boules ne sont pas confondues par le plan de gauche et donc que notre objet n'est pas invariant par ce plan)

C'est bien cela.

Bonjour,
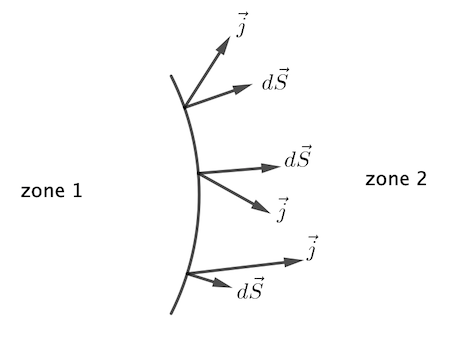
J'ai une dernière question (qui ne concerne pas les plans de symétries !), quand on écrit , est-ce que et sont orientés dans la même direction et dans le même sens ?

Bonjour,

Pour moi, c'est plutôt l'orientation de qui compte : comparez, en prenant un système fermé pour simplifier, le vecteur surface orienté vers l'extérieur ou l'intérieur.
Dans le premier cas, on obtiendra I sortant, dans le deuxième I entrant.

Cela veut donc dire que selon l'orientation que l'on a choisi pour la surface fermé et sont dans le même sens ou de sens opposés, néanmoins ils sont tout le temps dans la même direction.

Dans quel cas vous placez-vous ?

Si vous prenez un cas un tant soit peu général, la direction de est variable, et I n'a pas de direction : il va de la zone 1 vers la zone 2.

Pour parler de direction de I, je ne vois que l'approximation filiforme, et dans cas oui, mais de toute manière dans ce cas, il n'y a qu'une direction possible.