Niveau licence

physique statistique

Posté par
handa 04-12-15 à 15:02

salut
j'ai une démonstration dans le cours que je ne comprend pas ; merci de m'aider
Etude du paramagnétisme
cas d'une substance magnitique parfaite de N particules identiques
soit M le moment magétique et Mz sa projection sur (zz')

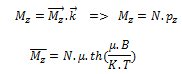
physique statistique

Posté par re : physique statistique 04-12-15 à 17:45

Le spin de chaque particule ne peut avoir comme énergie que deux valeurs et uniquement deux soit $+\mu B$ soit $-\mu B$ .

Il faut savoir que le spin "préfère" les états de plus basse énergie, le spin préfère avoir l'énergie $-\mu B$ que $+\mu B$ .

Le truc c'est qu'il y a une autre forme d'énergie, une énergie thermique : $kT$ . Cette énergie tend à vouloir faire que le spin prenne indifféremment les deux valeurs.

Il faut donc traduire en équation cette compétition entre ces deux formes d'énergies.

Ici intervient l'aspect probabiliste par l'introduction de la fonction de partition qui dit grosso modo que la probabilité est liée à cette compétition entre ces deux énergies.

Donc :
L'énergie totale U est la somme de $N\mu B$ pondéré par une certaine probabilité et de $-N\mu B$ pondéré par une certaine probabilité.

$U = N\mu B e^{\frac{\mu B}{kT}}+ -N\mu B e^{\frac{-\mu B}{kT}}$

U doit être normalisée par la fonction de partition $z= e^{\frac{\mu B}{kT}}+ e^{\frac{-\mu B}{kT}$
Soit $z=2ch(\frac{\mu B}{kT})$

Donc $U=-NB\mu sh(\frac{\mu B}{kT})/ch(\frac{\mu B}{kT})$
Et comme $U=-M_zB$
Tu retrouves le résultat de cours.