Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

physique mecanique

Posté par
Adou 09-02-16 à 22:53

bon soir s'il vous plais de votre aide pour débuter pour débuter mon exercice
Exercice une particule Mdans le plan xoy.sa vitesse est definie par =A+B
a)déterminer  l'équation de la trajectoire en cordonnées polaire en fonction de A et B
sachant qu'a l'instant initial r=1met =0
b)on choisit A=3B.déterminer l'équation cartésienne de la trajectoire
c)déterminer dans le même condition l'équation cartésienne de l'hodographe
Merci d'avance
c'est un devoir a rendre demain        

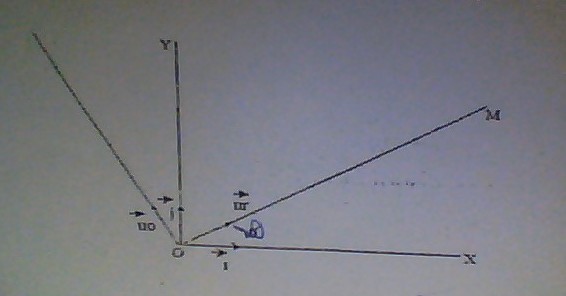
physique mecanique

Posté par
Adoure : physique mecanique 09-02-16 à 22:55

c'est un seul et non deux

Posté par
Adoure : physique mecanique 10-02-16 à 21:41

s'il vous plais guide moi

Posté par
Adoure : physique mecanique 11-02-16 à 21:34

s'il vous plais guider moi

Posté par
vanoisere : physique mecanique 11-02-16 à 21:43

Bonsoir,
ta formule de la vitesse n'est pas vraiment compréhensible. Peux-tu la réécrire ?

Posté par
vanoisere : physique mecanique 11-02-16 à 23:32

Un vecteur  vitesse s'exprime habituellement soit en coordonnées cartésiennes, c'est à dire dans la base \left(\overrightarrow{i},\overrightarrow{j}\right), soit en coordonnées polaires, c'est à dire dans la base \left(\overrightarrow{u_{r}},\overrightarrow{u_{\theta}}\right). La formule que tu fournis est très inhabituelle. L'expression ne serait-elle pas : \overrightarrow{v}=A\cdot\overrightarrow{u_{\theta}}+B\cdot\overrightarrow{u_{r}} ou \overrightarrow{v}=A\cdot\overrightarrow{u_{r}}+B\cdot\overrightarrow{u_{\theta}}  ?

Posté par
Adoure : physique mecanique 12-02-16 à 17:12

bon soir
voila l'expression de =Asmb]vectu[/smb]+B

Posté par
vanoisere : physique mecanique 13-02-16 à 00:34

Bonsoir,
voici quelques indications :

\overrightarrow{j}=\cos\left(\theta\right)\overrightarrow{u_{\theta}}+\sin\left(\theta\right)\overrightarrow{u_{r}}\quad donc\quad\overrightarrow{v}=\left[A+B\cos\left(\theta\right)\right]\overrightarrow{u_{\theta}}+B\sin\left(\theta\right)\overrightarrow{u_{r}}
L'expression générale du vecteur vitesse en coordonnées polaire est :

\overrightarrow{v}=r\frac{d\theta}{dt}\overrightarrow{u_{\theta}}+\frac{dr}{dt}\overrightarrow{u_{r}}
Par identification et en remarquant : \frac{dr}{dt}=\frac{dr}{d\theta}\cdot\frac{d\theta}{dt}, on obtient le système :

\begin{cases} \\ \frac{dr}{d\theta}\cdot\frac{d\theta}{dt}=B\sin\left(\theta\right)\\ \\ r\frac{d\theta}{dt}=A+B\cos\left(\theta\right)\\ \\ \text{rapport membre à membre en supposant \ensuremath{\frac{d\theta}{dt}\neq0} }\\ \\ \frac{\frac{dr}{d\theta}}{r}=\frac{B\sin\left(\theta\right)}{A+B\cos\left(\theta\right)} \\ \end{cases}
En remarquant que -B.sin()  est la dérivée de [A+B.cos(), l'intégration de la relation précédente conduit à :


\ln\left(r\right)=-\ln\left(|A+B\cos\left(\theta\right)|\right)+\ln\left(C\right)\quad\text{avec C : constante positive}
soit :

r=\frac{C}{|A+B\cos\left(\theta\right)|}
Puisque r = 1m pour =0, C est numériquement égal à (A+B) ; je n'écris pas C = A+B car C et (A+B) n'ont pas la même dimension physique.
Je te laisse continuer, la suite est facile... N'oublie pas pour finir de vérifier que \frac{d\theta}{dt}\neq0\quad\forall t car cette hypothèse a été utilisée pour obtenir l'équation de la trajectoire.

Posté par
Adoure : physique mecanique 14-02-16 à 12:05

s'il vous plais un peu d'explication sur l'expression  général du vecteur polaire  

Posté par
vanoisere : physique mecanique 14-02-16 à 12:24

Bonjour,
Si tu écris le vecteur position sous la forme :

\overrightarrow{OM}=r\cdot\overrightarrow{u_{r}}
On démontre en cours que l'expression du vecteur vitesse de M est :

\overrightarrow{v}=\frac{d\overrightarrow{OM}}{dt}=\frac{dr}{dt}\cdot\overrightarrow{u_{r}}+r\cdot\frac{d\theta}{dt}\cdot\overrightarrow{u_{\theta}}
J'utilise les notations du schéma que tu as fourni. Je ne peux pas en quelques lignes sur ce forum refaire un cours complet sur le sujet...

Posté par
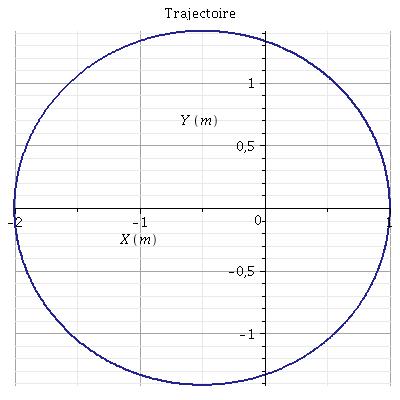
Adoure : physique mecanique 14-02-16 à 12:36

merci la vaniose .comment on peut obtenir l'équation  cartésienne de l'hodographe

Posté par
vanoisere : physique mecanique 14-02-16 à 18:26

Tu as tracé la trajectoire du point M et montré qu'il s'agit d'une ellipse ? As-tu étudié en cours l'équation polaire d'une ellipse ?
L'hodographe est le lieu des points P du plan de la trajectoire tel qu'à chaque instant :

\overrightarrow{V_{(M)}}=\overrightarrow{OP}
Les coordonnées du point P sont donc Vx et Vy : les coordonnées cartésiennes du vecteur vitesse du point M. En remarquant :

\overrightarrow{u_{\theta}}=\cos\left(\theta\right)\overrightarrow{j}-\sin\left(\theta\right)\overrightarrow{i}
L'expression du vecteur vitesse de M peut s'écrire :

\overrightarrow{V_{(M)}}=A\overrightarrow{u_{\theta}}+B\overrightarrow{j}=-A\sin\left(\theta\right)\overrightarrow{i}+\left[B+A\cos\left(\theta\right)\right]\overrightarrow{j}=B\left[-3\sin\left(\theta\right)\overrightarrow{i}+\left(1+3\cos\left(\theta\right)\right)\overrightarrow{j}\right]
Cela donne :

\begin{cases} \\ v_{x}=-3B\sin\left(\theta\right)\\ \\ v_{y}=B\left[1+3\cos\left(\theta\right)\right] \\ \end{cases}
Ensuite, tu isoles sin() d'une part, cos() d'autre part .Tu obtiens la relation entre Vx et Vy en écrivant :
sin2()+cos2()=1 à chaque instant.
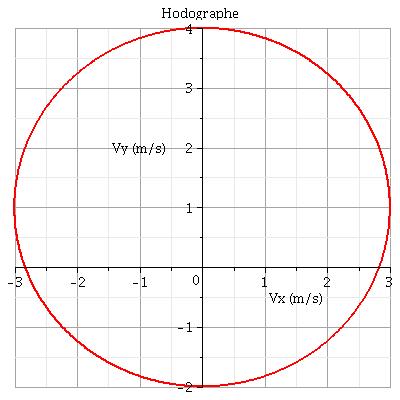
Je te laisse démontrer qu'il s'agit d'un cercle de rayon 3Bm/s et de centre de coordonnées (0,-B).
Voici en dessous l'hodographe ainsi que la trajectoire. Pour l'hodographe, j'ai choisi pour le tracé : B=1m/s.

physique mecanique

physique mecanique

Posté par
vanoisere : physique mecanique 15-02-16 à 15:37

Bonsoir,
Erreur de signe de ma part à l'avant-dernière ligne :
"Je te laisse démontrer qu'il s'agit d'un cercle de rayon 3Bm/s et de centre de coordonnées (0,B)." (et pas -B)

Posté par
Adoure : physique mecanique 18-02-16 à 22:09

bon soir vaniose je peux avoir l'expression de ton  équation cartésienne de la trajectoire

Posté par
vanoisere : physique mecanique 18-02-16 à 23:07

Bonsoir,
tu pars de l'équation polaire déjà fournie où r est mesuré en mètres :

r=\frac{C}{|A+B\cos\left(\theta\right)|}=\frac{4}{3+\cos(\theta)}
tu obtiens les coordonnées cartésiennes à partir des relations :

x=r\cdot\cos\left(\theta\right)\quad et\quad y=r\cdot\sin\left(\theta\right)
Tu exprimes le cosinus en fonction de x, le sinus en fonction de x et y puis tu écris la relation bien connue :

\cos^{2}\left(\theta\right)+\sin^{2}\left(\theta\right)=1
Tu vas obtenir l'équation d'une ellipse de centre O' dont les coordonnées sont (-0,5 ,0) dont les axes de symétrie sont parallèles aux axes (Ox) et (O,y). Il est en effet possible d'écrire l'équation cartésienne de la trajectoire sous la forme :

\boxed{\frac{\left(x+0,5\right)^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1}
On peut alléger sensiblement les calculs  à condition de bien connaître son cours sur les propriétés des ellipses : paramètre, excentricité, demi grand axe, demi petit axe...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !