Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

physique des vibrations

Posté par
juju0305 21-02-19 à 18:15

Bonjour,

J'ai un exercice de physique des vibrations à faire et je bloque complètement, pouvez vous m'aiguiller dans mon travail ?

Voici l'énoncé :

Pour les pendules considérés dans cette partie, on demande la pulsation  ω0 des petites oscillations, avec, selon  le cas, des questions spécifiques précisées dans chaque cadre. On  pourra utiliser diverses méthodes (PFD, énergie,…)
a) w0 pendule vertical vers le bas
La réponse est : \sqrt{\frac{2K}{M}\left(\frac{a}{l} \right)^{2} + \frac{g}{l}}
je reconnais bien le g/l du pendule classique mais je n'arrive pas à retrouver le reste de la formule...

Merci d'avance

Posté par
vanoisere : physique des vibrations 21-02-19 à 18:22

Bonjour
Ne s'agirait-il pas d'un pendule dont la tige serait reliée à deux ressorts horizontaux ?

Posté par
juju0305re : physique des vibrations 21-02-19 à 18:30

bonjour,

oui mea culpa je n'avais pas remarqué que l'image n'était pas liée au topic :/
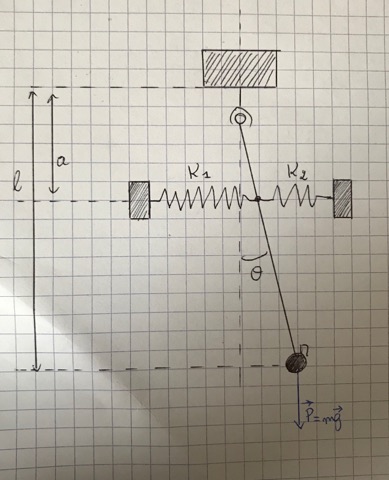
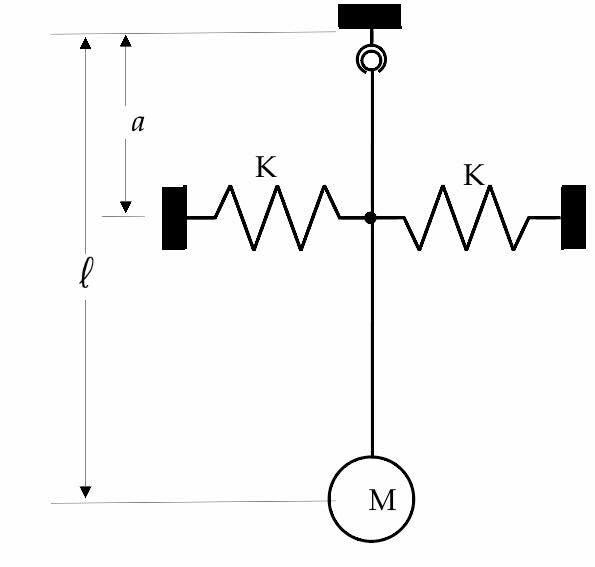
il s'agit en effet d'un d'un pendule dont la tige est reliée à deux ressorts horizontaux.

physique des vibrations

Posté par
vanoisere : physique des vibrations 21-02-19 à 18:54

J'ai un peu l'entraînement . S'il te faut faire la démonstration, tu as le choix entre deux méthodes :
1° : appliquer le théorème du moment cinétique au pendule seul ;
2° : raisonner sur la conservation de l'énergie mécanique du système constitué du pendule et des deux ressorts.
Il faut bien sûr supposer l'amplitude des oscillations faibles.

Posté par
juju0305re : physique des vibrations 21-02-19 à 20:48

merci !
en utilisant le théorème du moment cinétique, je retrouve bien l'expression \sqrt{\frac{g}{l}} grâce à l'équa diff \ddot{\theta } + \frac{g}{l}sin(\theta ) mais je ne retrouve pas \sqrt{\frac{2K}{M}\left(\frac{a}{l} \right)^{2}} ...

Posté par
vanoisere : physique des vibrations 21-02-19 à 20:59

Pour une déviation d'angle faible et positive, le ressort de droite subit un raccourcissement égal à a. et le ressort de droite subit un allongement aussi égal à a.. Les deux tensions agissent dans le même sens...

Posté par
juju0305re : physique des vibrations 21-02-19 à 21:03

je pense qu'avec ceci je peux obtenir le facteur (a/l)² mais j'ai encore du mal à voir d'où vient le facteur 2K/M...

Posté par
vanoisere : physique des vibrations 21-02-19 à 22:41

Commence par faire une schéma avec le pendule écarté d'un angle . Représente sur le schéma les différentes forces extérieures appliquées puis applique au pendule le théorème du moment cinétique. Tu peux poster le schéma sur le forum.

Posté par
juju0305re : physique des vibrations 22-02-19 à 17:08

une fois le pendule modélisé décalé, j'obtiens ce schéma.

physique des vibrations

Posté par
juju0305re : physique des vibrations 22-02-19 à 17:29

le facteur \sqrt{\frac{2K}{M}\left(\frac{a}{l} \right)^{2}} est-il obtenu par la résolution :
\frac{d}{dt}(Ec+Ep) = M\dot{x}+2Kx=0 \Rightarrow \sqrt{\frac{2K}{M}}
avec : Ec = \frac{1}{2}M\dot{x}^{2} et Ep = 2 * \frac{1}{2}K(x-0)^{2} pour prendre en compte les 2 ressorts.
la solution de l'équa diff est alors : \sqrt{\frac{2K}{M}}

Posté par
vanoisere : physique des vibrations 22-02-19 à 18:25

Énergie cinétique du pendule :

E_{c}=\frac{1}{2}m.v^{2}=\frac{1}{2}m.l^{2}.\left(\frac{d\theta}{dt}\right)^{2}

Énergie potentielle de pesanteur, en choisissant arbitrairement l'altitude nulle à la position d'équilibre stable :

E_{pp}=m.g.l.\left[1-\cos\left(\theta\right)\right]

L'angle étant très petit :

\cos\left(\theta\right)\approx1-\frac{\theta^{2}}{2} ; d'où l'expression de l'énergie potentielle de pesanteur :

E_{pp}=\frac{1}{2}m.g.l.\theta^{2}

Comme déjà dit, la variation de longueur de chaque ressort est a.\theta, d'où l'expression de l'énergie potentielle élastique des deux ressorts :

E_{pe}=2.\left(\frac{1}{2}.k.a^{2}.\theta^{2}\right)

La somme de ces trois énergies est l'énergie mécanique Em qui se conserve. Tu aboutit au résultat recherché en écrivant :

\frac{dE_{m}}{dt}=0\;\forall t
Je te laisse terminer...

Posté par
juju0305re : physique des vibrations 22-02-19 à 19:14

j'obtiens l'équation :
ml^{2}\ddot{\theta }^{2}+mgl\dot{\theta ^{2}}+2Ka^{2}\dot{\theta }^{2} = 0
ne reste-t-il "plus qu'à" la résoudre pour obtenir le résultat souhaité ?

Posté par
vanoisere : physique des vibrations 22-02-19 à 19:45

Revois bien ton cours sur le sujet et surtout  : tu as sûrement traité en cours des exemples similaires car tu es vraiment très loin du compte pour quelqu'un qui poste au niveau enseignement supérieur.

Posté par
vanoisere : physique des vibrations 22-02-19 à 19:47

Revois aussi ton cours de mathématiques sur les dérivées de fonctions de fonctions...

Posté par
juju0305re : physique des vibrations 22-02-19 à 20:41

Merci j'ai réussi à trouver la solution demandée.
Merci pour votre patience, vos réponses et désolée de vous avoir dérangée...

Posté par
vanoisere : physique des vibrations 22-02-19 à 21:39

Pas de problème pour le dérangement  !
Bon courage pour revoir ton cours.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !