Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... AutreForum autre de supérieur PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau autre
Partager :

Physique Classique mécanique du point

Posté par
nicom 14-11-12 à 14:32

Bonjour,

j'ai des petits problèmes dans la résolution d'un exercice :
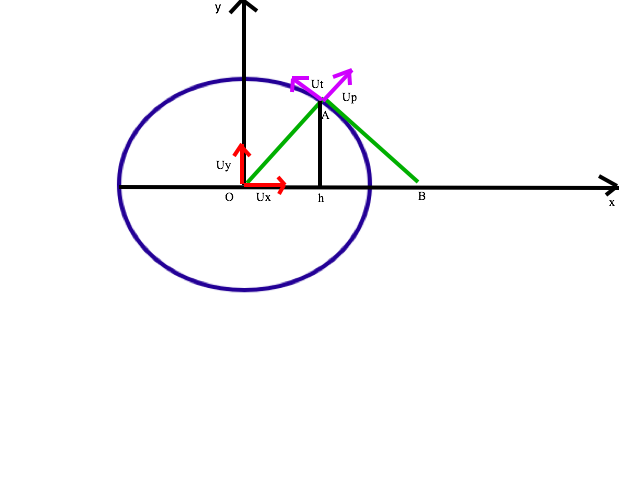
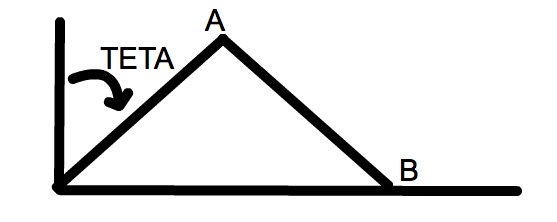
une double échelle OAB (le point O est situé à l'origine des "axes" en bas à gauche de la figure) appuyée au bas d'un mur tombe, le point B glisse sur le sol.
Vitesse angulaire Teta(t) de 10°/s et Teta(t=0)=15°.

Question Donner le vecteur vitesse et accélération du point B.

Résolution deux méthodes :

méthode 1:
D'après l'énoncé : Téta(t)=\frac{10\pi}{180}+\frac{15}{180}
OB = 2OAsin(Teta)
\frac{d\overrightarrow{OB}}{dt}=\frac{10}{180}2OAcos(\frac{10\pi}{180}+\frac{15}{180})
\frac{d^2\overrightarrow{OB}}{dt^2}=-\frac{10}{180}^22OAsin(\frac{10\pi}{180}+\frac{15}{180})

Problème accélération négative... sens physique ?
(ceci correspond à la résolution du problème par le bouquin)

Ma méthode est légèrement différente (et plus longue)
Sachant qu'il y a un mur le déplacemeent du point B est le même que celui du point A selon ux.
On a donc : \overrightarrow{OA}=-OA\times cos(Teta)\times \overrightarrow{ux}
\frac{\overrightarrow{dOA}}{dt}=-OA\frac{dOA}{dt}cos(Teta)\overrightarrow{ux}
\frac{\overrightarrow{d^2OA}}{dt^2}=-OA(\frac{dOA}{dt})^2sin(Teta)\overrightarrow{ux}

Et ici, c'est le drame, la vitesse et l'accélération sont négatives.
Au final je pensais ajouter la distance entre le projeté de OA sur ux à T=0 et le point B pour obtenir OB=f(t).

Pourriez-vous m'aider à trouver la/les erreur de méthodologie ?
En vous remerciant d'avance,
nicom.

Physique Classique mécanique du point

Posté par
Coll Moderateurre : Physique Classique mécanique du point 14-11-12 à 15:49

Bonjour,

Je trouve que ce que tu as recopié de la réponse du livre a plusieurs erreurs :
. il manque le temps
. il manque
. il manque des carrés (y compris 2)

Quelle est la difficulté avec le sens physique ?

Il est évident que la vitesse diminue
et il est tout aussi évident que l'accélération est négative.

Imagine ce qui se passerait si le point B était sur un rail et que le point A ne s'arrête pas au sol mais puisse continuer vers le bas...

Posté par
nicomre : Physique Classique mécanique du point 14-11-12 à 17:25

Merci beaucoup d'avoir répondu si vite !!
S'il vous plaît veuillez excusez les erreurs de transcription livre -> ordi.

Il me semble que nous parlons ici du déplacement du point B.
Si l'échelle tombe le point B se déplace vers le côté droit de la figure soit + l'infini.
Évidement il est limité par la taille de l'échelle et le fait que lorsque l'échelle traverse l'axe des x le mouvement se fait alors dans l'autre sens.

Première remarque : Il est évident que la vitesse diminue.
Pourquoi ? Il n'y a pas de frottement ni de force de rappel (type ressort). Il me semble que la vitesse devrait augmenter puis changer brusquement de sens et s'annuler pour augmenter de nouveau.

Deuxième remarque: Il est évident que l'accélération est négative.
L'accélération négative signifie que le mouvement est ralentit à mesure que le temps augmente.

Je ne comprends pas pourquoi.
Si on atteint /2 ok il revient, mais avant (entre 0 et pi/2) les point B se déplace donc vitesse et accélération dans le même sens.

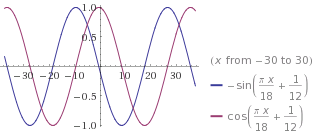
Voir trace des courbes : ** lien vers l’image effacé **


Edit Coll : tu peux placer les images sur le serveur de l' en respectant la FAQ   

Posté par
Coll Moderateurre : Physique Classique mécanique du point 14-11-12 à 17:33

L'accélération est négative parce que la vitesse diminue toujours.

La vitesse diminue : regarde le tracé des courbes pour t compris entre 0 s et 7,5 s si tu n'es pas convaincu(e)
Mais c'est "physiquement" évident si tu considères la rotation du point A autour du centre O

Posté par
nicomre : Physique Classique mécanique du point 14-11-12 à 17:53

Je suis entièrement d'accord avec vous sur l'interprétation des résultats et des courbes.


Avant 7,5s le vecteur vitesse est dirigé vers le 0 comme l'accélération.
Pourtant \vec{OB} est dans le sens inverse.
Or pour moi un mouvement se fait dans le sens du vecteur vitesse.

J'admet qu'ici l'évidence physique m'échappe... Peut être que ça viendra un jour mais là...

En tout cas merci beaucoup pour votre aide/patience.
Je repasserai probablement bientôt avec de nouveaux problèmes...

Physique Classique mécanique du point

Posté par
nicomre : Physique Classique mécanique du point 14-11-12 à 17:56

Ahhhhhh j'ai compris..... !!!

Le vécteur vitesse est dans le sens du mouvement puisqu'il est positif !!
Il dimniue simplement au cours du temps.

Mais pourquoi ?
Considérons la vitesse de rotation du point A qui est croissante pour tout t, je ne voit pas ne quoi cela prédétermine le fait qu'il y ai un mouvement amortit.

Posté par
Coll Moderateurre : Physique Classique mécanique du point 14-11-12 à 18:03

\vec{OB} est dans le sens inverse de quoi ?

La courbe rouge, la vitesse, est toujours positive mais décroissante ; qu'elle diminue ne signifie pas qu'elle soit négative...

La courbe bleue, l'accélération est toujours négative, car la vitesse diminue...

Posté par
nicomre : Physique Classique mécanique du point 14-11-12 à 18:20

Oui, j'ai compris entre temps ^^

Du coup en résumé :
- \vec{OB} est dirigé vers l'infini
- \frac{d\vec{OB}}{dt} est dirigé vers l'infini
- \frac{d^2\vec{OB}}{dt^2} est dirigé vers 0.
- la vitesse de rotation du point A : Teta augmente avec t (relation affine).
Donc on a un mouvement à vitesse constante.

Je ne vois pas en quoi il est physiquement évident d'observer un mouvement amorti.

Posté par
Coll Moderateurre : Physique Classique mécanique du point 14-11-12 à 18:27

Dirigé vers l'infini ? Dirigé vers zéro ?
Ces vecteurs ont des composantes (pour 0 t 7,5 s) respectivement :
. positive
. positive ou nulle
. négative
____________________

L'évidence, ou son absence, est difficile à transmettre.

Pense à la transformation d'un mouvement de rotation en un mouvement rectiligne de va-et-vient...

Posté par
nicomre : Physique Classique mécanique du point 14-11-12 à 18:59

Citation :
Pense à la transformation d'un mouvement de rotation en un mouvement rectiligne de va-et-vient...


En fait je crois que je comprends mais il reste un verrou que j'ai du mal à situer et qui ne veux pas sauter.
Je comprends le mouvement du point A projeté sur ux.
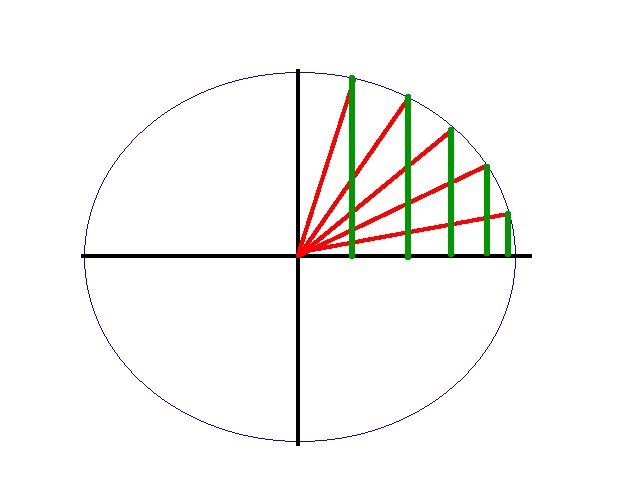
Je le visualise de la manière suivante : pour un échantillonnage de temps constant nous allons observer une réduction de la distance entre les points à mesure que le temps augmente, ce qui traduit l'augmentation de vitesse en rotation.

Cela signifie que le point B s'écarte d'abord beaucoup puis de moins en moins. On a donc affaire à un mouvement amorti.

Cependant j'ai quand même du mal à faire le lien avec la vitesse et l'accélération, même si mathématiquement c'est juste.

Juste une dernière question, que pensez-vous de ma méthode (incomplète) de résolution (qui utilise le repère tournant en fait) ?  

En tout cas merci beaucoup pour tout.
J'ai (ré)appris, entre autres, qu'il faut que je sois beaucoup plus attentif au sens des vecteurs lorsque j'ai affaire à des sinus/cosinus.

Posté par
Coll Moderateurre : Physique Classique mécanique du point 14-11-12 à 19:20

Je suis désolé mais cette deuxième "méthode" me semble complètement fausse et je ne la comprends pas.
___________

Je t'en prie.
À une prochaine fois !

Posté par
nicomre : Physique Classique mécanique du point 14-11-12 à 21:57

En fait ma méthode est la suivante :

Je place dans le repère tournant \vec{OA} :
On a par définition \vec{OA}=r\vec{up} avec \vec{up} vecteur unitaire porté par (OA) en direction du bord du cercle et r le rayon du cercle.

Soit Theta(t) la fonction décrivant la variation angulaire du point OA tel que :  Theta(t)=\frac{10\pi}{180}t+\frac{15}{180}

Vécteurs de base : \vec{up}=cos(Theta)\vec{ux}+sin(Theta)\vec{uy}
\vec{u_t}=-sin(Theta)\vec{ux}+cos(Thetha)\vec{uy}

On a \vec{OA}=r\vec{up}=rcos(Theta)\vec{ux}+rsin(Theta)\vec{uy}

\frac{\vec{dOA}}{dt}=r\frac{dTheta}{dt}\vec{u_t} avec u_t vecteur de base orthonormé à \vec{up} dans le sens trigonométique (dérivé vrai si r constant).

Enfin : \frac{\vec{d^2OA}}{dt^2}=r\frac{d^2Theta}{dt^2}\vec{u_t}-r(\frac{dTheta}{dt})^2\vec{u_p}

Le mouvement qui nous intéresse ici n'a lieu que selon le vecteur unitaire \vec{ux} :
\frac{\vec{dOA}}{dt} =-r\frac{dTheta}{dt}sin(Thetha)\vec{ux}
\frac{\vec{d^2OA}}{dt^2} =-r(\frac{dTheta}{dt})^2cos(Thetha)\vec{ux} (car pas d'accélération du mouvement de révolution)

Donc normalement là j'ai toutes les équations pour m'en sortir.
Demain j'essaye de finir de résoudre le problème en appliquant les relations au point B.

D'ailleurs j'ai enfin compris pourquoi le mouvement est amorti cf figure (temps d'échantillonnage constant).
En fait le mouvement est amortit parce que le mouvement est de type sinusoïdal un point c'est tout ^^
(Il m'a quand même fallut une après midi pour arriver à ce résultat...)

Physique Classique mécanique du point

Posté par
Coll Moderateurre : Physique Classique mécanique du point 15-11-12 à 08:28

"Pourquoi faire simple quand on peut faire compliqué ?" et ainsi avoir la chance de pouvoir se tromper toutes les deux lignes...

Je trouve que cela commence très mal (je n'ai pas tout lu...) :

\large \theta(t) est faux.

Quel est l'axe que tu nommes Ox et celui que tu nommes Oy ?

Posté par
nicomre : Physique Classique mécanique du point 27-11-12 à 20:26

Bonjour !!

Alors tout cela commence à dater, mais je n'ai malheureusement eu que peu de temps pour moi.

Voici ma résolution qui est très simple finalement.
Je vais faire de mon mieux pour copier sans erreur vu que j'ai un peu de temps devant moi.

Nous sommes dans une base orthonormée (o,x,y) dont les vecteur de bases sont (\vec{ux},\vec{uy}).

Soit C le cercle de centre O tel que [OA] est un rayon noté r.

Soit les vecteurs de base tournants définis au point A par: \vec{up} colinéaire à \vec{OA} et \vec{ut} normal à \vec{up} dans le sens trigonométrique.

Soit h le projeté de A sur (Ox) et l'angle hÔA est noté Teta.

On a quelque soit Teta par définition :
- \vec{up}=cos(Teta)\vec{ux}+sin{Teta)\vec{uy}
- \vec{ut}=-sin(Teta)\vec{ux}+cos(Teta)\vec{uy}

Le mouvement est circulaire Teta varie de 10°/s et à l'origine des temps mesure 15°.
On a donc : Teta(t)=\frac{-10\pi}{180}+\frac{65\pi}{180} en radians. Il faut ici garder en tête que notre base de vécteur tournant est posée dans le sens trigonométrique (donc Teta(0)=hÔB=90-15=65°).

\vec{OA}= r\vec{up}

Étant donné que r ne varie pas on a :
\frac{d\vec{OA}}{dt}=r\frac{d(Teta)}{dt}\vec{ut}

Et que le mouvement circulaire n'est pas accéléré (\frac{dTeta}{dt}=\frac{10\pi}{180} qui est une constante), on a alors:
\frac{d^2\vec{OA}}{dt^2}=-r(\frac{d(Teta)}{dt})^2\vec{up}

On cherche l'équation du mouvement au point B. Ici se situe l'astuce, en fait étant donné la symétrie du système lorsque OA tombe il entraîne AB dans son mouvement. Le triangle isocèle OAB reste isocèle quel que soit t puisque le mouvement s'effectue sans glisser ([oh]=[hB]).
Le mouvement de B est uniquement selon (o,x) et on note P[\vec{OA},\vec{ux}] le projeté du vecteur OA sur le vecteur de base ux.

On a donc \vec{OB}=2P[\vec{OA},\vec{ux}]

Ainsi on en déduit les équations du mouvement de OB:
-Position : \vec{OB}=2\vec{Oh}=2rcos(Teta)\vec{ux}
-Vitesse : \frac{d\vec{OB}}{dt}=-2r\frac{dTeta}{dt}sin(Teta)\vec{ux}
-Position : \frac{d^2\vec{OB}}{dt^2}=-2r(\frac{dTeta}{dt})^2cos(Teta)\vec{ux}

En conclusion :
- La position croît dans l'intervalle [\frac{\pi}{2};0] ce qui est cohérent.
- La vitesse diminue tout en restant positive (\frac{d(Teta)}{dt}<0).
- L'accélération est négative, le point B décélère, ce qui est cohérent avec la conversation que nous avons eu avant.

Alors maintenant, pourquoi cette méthode ?
Elle me semble plus rigoureuse car applicable quelque soit le problème.
Après c'est aussi parce que cela permet d'appliquer le cours sur les vecteurs tournant que je maîtrise encore mal.

En tout cas je veux encore vous remercier de m'avoir répondu.
J'espère que cela pourra aider quelqu'un à l'avenir.

Bonne soirée et à bientôt,
Nicolas

Ps: Si vous voyez des problèmes dans la rigueur des maths je serais ravi d'avoir votre avis afin de m'améliorer.

Physique Classique mécanique du point

Posté par
Coll Moderateurre : Physique Classique mécanique du point 28-11-12 à 07:47

Je pense que cela n'aidera personne à l'avenir tant il y a d'erreurs.

Tu n'as pas corrigé \theta (t) qui est toujours faux ; alors, le reste...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !