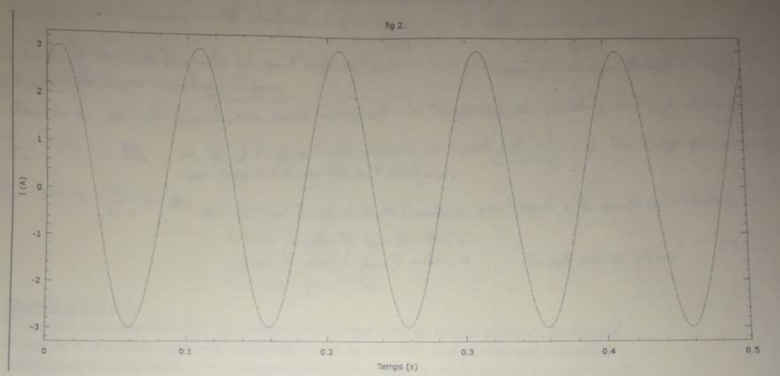
Le courant, dont la mesure est rapporté dans ton graphique est visiblement une fonction sinusoïdale du temps:

qui peut donc s'écrire  

  est "la phase à l'origine": c'est la phase de la fonction sinusoïdale pour t = 0



A toi de jouer

Merci beaucoup pour votre réponse !

Donc si je reprends votre formule, Imax = 3 A, i en t=0 donne 2,7 A. Ce que je ne comprends pas c'est que l'on cherche la phase à l'origine donc comment je suis supposé trouver sin Φ ?

Encore merci pour l'aide que vous m'accordez, bonne journée.

Ah j'ai finalement peut être trouvé, sin Φ = i(t=0)/I max ? Ce qui donnerait sin Φ = 2,7/3 ?

Arc sin 2,7/3 = 64,15° ?

Effectivement

Comme     on a bien

Soit



En toute rigueur cela ne te permet pas de déterminer complètement qui d'ailleurs s'exprime en radians et non pas en degrés, la pulsation s'exprimant en radian pas seconde et l'expression t+ devant être homogène

Donc si   alors ou bien

Pour déterminer laquelle de ces 2 valeurs choisir il faut s'intéresser à la variation du courant à l'origine



Donc à l'origine



Tu vois sur le graphe qu'à l'origine la variation du courant est croissante, il te faut donc sélectionner la valeur de dont le cosinus est positif.

On a bon?

Merci pour votre réponse très claire j'ai tout compris excepté une petite chose.

J'ai bien trouvé la valeur 1,12 rad mais ne j'arrive pas à comprendre comment trouver 2,02 rad avec ma calculette.

Le cosinus de 2,02 rad donnant une valeur négative, je dois choisir la première valeur soit Φ = 1,12 rad.

Ai-je bon ? Merci encore !

Bon tu as sélectionné la bonne valeur c'est déjà cela.

J'espère que tu as compris également pourquoi il fallait choisir cette valeur, car c'est la seule qui permet de retrouver un di/dt > 0 à l'origine des temps, comme le graphe l'indique

Maintenant pourquoi ta calculette retourne 1,12, ... parce qu'elle est bien élevée et retourne l'antécédent de 0,9 sur l'ensemble de définition de Arcsin qui est -pi/2; +pi/2

maintenant tu sais aussi que la fonction sinus est périodique de période 2pi

Et donc pour trouver toutes les solutions x de l'équation sin(x) = a  il faut scruter un intervalle de longueur 2pi, en optimisant éventuellement en se souvenant que sin(pi-x) = sinx