Inscription / Connexion Nouveau Sujet
PFD sur une équation paramétrée
Bonjour,
Dans le cadre de mon TIPE, je n'arrive pas à résoudre un problème : j'étudie un looping dans une montagne russe, dont la forme des rails est représentée par une clothoïde et je n'arrive pas à appliquer le PFD sur cette trajectoire.
Je m'explique : je fais mon BDF : le poids, la réaction du support et les forces de frottements. J'applique mon PFD. Je souhaite ensuite obtenir la vitesse selon le vecteur directeur tangent aux rails, mais je n'arrive pas à éliminer la réaction du support, car si je projette selon le vecteur tangent aux rails, je ne sais pas retomber sur ma vitesse...
J'espère avoir été clair...
Auriez-vous des idées ?
Merci beaucoup !
Bonjour
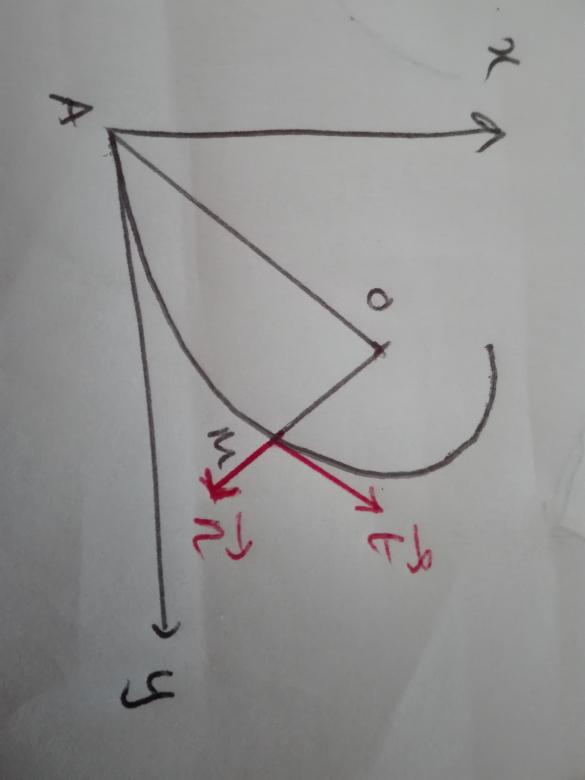
La projection de l'accélération suivant la tangente et la normale à la trajectoire puis l'application des lois de Coulomb sur les frottements solides peuvent peut-être t'aider...
En appelant N la réaction normale des rails et T la force de frottement, cela donne :
En appelant l'angle entre le vecteur poids et le vecteur unitaire
normal à la trajectoire et orientée vers l'extérieur de la trajectoire comme sur ton schéma, cela donne
où est le rayon de courbure de la trajectoire. Ensuite plusieurs hypothèse peuvent être faites. J'ai parlé précédemment de frottements solides... Ils sont peut être négligeables devant les frottements dus à l'air. Compte tenu des vitesses obtenues, on peut alors poser : T=k.v2...
Tout cela n'est pas simple...