Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... DoctoratForum Supérieur de doctorat PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau doctorat
Partager :

PFD dans un repère cylindrique

Posté par
Nightingale7 07-08-20 à 15:39

Bonjour à tous,
Dans le cadre de ma thèse en physique, je dois résoudre le principe fondamental de la dynamique dans un repère cylindrique.
Ainsi, je dois résoudre ce système d'équations et obtenir les fonctions temporelles pour chacune des composantes.

\begin{array}{rcr} \\     \frac{d^2r}{dt^2} - r \frac{d\theta}{dt} & = & \frac{qE_r}{m} \\ \\     2 \frac{dr}{dt} \frac{d\theta}{dt} + r\frac{d^2\theta}{dt^2} & = & 0 \\ \\     \frac{d^2z}{dt^2} & = & \frac{qE_z}{m} \\   \end{array}

Ainsi, la dernière équation est complétement déliée des deux premières et donc z(t) est facilement trouvable, toutefois résoudre le système d'équa-diff qui couple r et \theta me semble très compliqué à résoudre...

Il s'agit d'un problème 2D d'un corps soumis à une unique accélération centrale (si on sépare le problème dans le plan (r, \theta)[sup][/sup] de la trajectoire dans la direction z
Note : $\frac{qE_r}{m}$est une constante


Est-ce que quelqu'un aurait un conseil à me donner sur l'approche à avoir pour cette résolution ?
Merci beaucoup,

Nightingale7

Posté par
vanoisere : PFD dans un repère cylindrique 07-08-20 à 16:07

Bonjour
La seconde équation est équivalente à r^{2}.\dot{\theta}=C, onstante que les conditions initiales permettent sans doute de déterminer.
Cela "découple" le système...

Posté par
Nightingale7re : PFD dans un repère cylindrique 07-08-20 à 17:33

Merci beaucoup pour votre réponse,
J'ai identifié cette constante des aires et j'imagine qu'il doit y avoir une astuce pour simplifier ce problème.
\frac{d(r^2\dot{\theta}}{dt}) = r(2\dot{r}\dot{\theta} + r\ddot{\theta}) = 0 et donc comme tu le dis,  r^2\dot{\theta} = C
J'ai identifié r\dot{\theta}^2 dans la composante radiale, j'imagine que l'on doit pouvoir introduire C et simplifier le problème.

En faisant :

Je pose : \frac{qE_r}{m} = A

\begin{cases} \\ \ddot{r} - A  =  r\dot{\theta}^2 \\ \\ 2 \dot{r} \dot{\theta} + r\ddot{\theta} =  0 \\ \end{cases} \Leftrightarrow \begin{cases} \\ (\ddot{r} - A)r^3  =  C^2 \\ \\ r^2\dot{\theta} =  C \\ \end{cases}\Leftrightarrow\begin{cases} \\ \ddot{r} - \frac{C^2}{r^3}   = A \\ \\ r^2\dot{\theta} =  C \\ \end{cases} r \neq 0

Cependant, à ce niveau ce sont mes compétences en math qui me font défaut, cette EDP est-elle facilement résoluble ?

Posté par
vanoisere : PFD dans un repère cylindrique 07-08-20 à 21:59

Concernant le mouvement dans le plan perpendiculaire à l'axe Oz : l'accélération est radiale de norme constante. Est-elle aussi centripète ? Si oui , la situation est simple : le mouvement dans ce plan est circulaire et uniforme sous réserve de conditions initiales cohérentes. L'accélération dans le plan devient simplement :

\overrightarrow{a}=\frac{d\Vert\overrightarrow{v}\Vert}{dt}\cdot\overrightarrow{u_{\theta}}-\frac{\Vert\overrightarrow{v}\Vert^{2}}{r}\cdot\overrightarrow{u_{r}}=\frac{q.E_{r}}{m}\cdot\overrightarrow{u_{r}}

avec : Er<0.

Le mouvement dans l'espace serait alors simplement un mouvement hélicoïdal...

Un peu plus de renseignements sur le problème étudié aiderait à tester le réalisme de cette hypothèse.

Posté par
vanoisere : PFD dans un repère cylindrique 08-08-20 à 07:54

Plutôt  :
q.Er<0
La force est radiale centripète.

Posté par
Nightingale7re : PFD dans un repère cylindrique 08-08-20 à 09:29

Merci pour ton aide vanoise,
Le problème posé est le suivant,
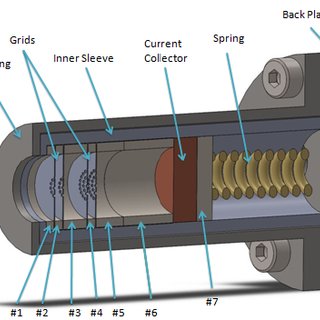
Je souhaite calculer la trajectoire d'un ion arrivant dans une sonde plasma (retarding potential analyser RPA). Cette sonde est un cylindre creux composé de 3 grilles successives. La première est polarisée à un potentiel de référence, à l'équilibre avec le plasma environnant, la deuxième est chargée negativement et a pour objectif d'empêcher les électrons d'entrée dans la sonde enfin, la dernière va faire un balayage en potentiel de 0V à 300V et sert de filtre en énergie pour les ions incidents.
De plus, les parois de ce RPA donc sur le cylindre dans mon cas d'étude restent au potentiel de référence (PJ).
Ainsi, ma façon de procéder et la suivante afin de calculer les trajectoires:
J'ai résolu la carte des champs électriques en maillant ma sonde. Pour simplifier le problème je les suppose constant dans une maille. Et donc je me retrouve dans la situation où dans chaque maille, ma particule est soumise à un champ électrique axial (direction z) et un champ électrique radial (qEr > 0)  d'où mon problème.
Je suis donc bien dans le cas d'une particule soumise à une force centrale dans le cas du mouvement plan radial, orthoradial.

PFD dans un repère cylindrique

Posté par
Nightingale7re : PFD dans un repère cylindrique 08-08-20 à 09:34

Mais pour revenir à ce que tu dis, mes conditions initiales sont les suivantes : les composantes de vitesses sont toutes non nulles.
La trajectoire dans le plan (r, \theta) décrit une spirale non ?
r \neq cst

Posté par
vanoisere : PFD dans un repère cylindrique 08-08-20 à 18:01

Je n'ai aucune  connaissance particulière sur les sondes à plasma. Ce que j'écris est donc à prendre avec réserve...
Mes connaissances en électrostatique me permettent cependant les remarques suivantes :
* un champ radial s'obtient entre deux électrodes cylindriques coaxiales de rayons différents portées à des potentiels différents et dans ce cas, la norme du vecteur champ n'est pas constante mais est inversement proportionnelle à r, la distance à l'axe.
* une électrode cylindrique longue ne crée pas de champ à l'intérieur du cylindre, sauf éventuellement au voisinage des extrémités du cylindre. On utilise parfois ce genre d'électrode pour protéger l'intérieur d'éventuels champs extérieurs perturbateurs.
* tu pourrais donc peut-être te concentrer sur l'influence des différentes grilles comme cela semble se faire dans les quelques études de sondes à plasma que j'ai pu trouver sur le net.
Encore une fois : sous toute réserve...

Posté par
gts2re : PFD dans un repère cylindrique 08-08-20 à 21:31

Bonjour,

Juste une incursion, j'ai l'impression que le champ n'est pas constant, mais constant dans une cellule et non pas dans la sonde.
Et dans ce cas c'est un problème numérique et non analytique.

Posté par
vanoisere : PFD dans un repère cylindrique 08-08-20 à 21:51

On trouve sur le net de nombreux documents analysant le rôle des différentes grilles. Ici par exemple :

Posté par
Nightingale7re : PFD dans un repère cylindrique 18-08-20 à 09:24

gts2, en effet tu as vu juste c'est un problème avant tout de physique appliquée dans une cellule de mon domaine de calcul. Dans cette cellule, les champs sont constants. Mon problème réside vraiment dans l'obtention de l'équation de la trajectoire dans cette cellule et c'est pour cela que je pense que c'est un problème de mathématiques...

Posté par
gts2re : PFD dans un repère cylindrique 18-08-20 à 10:23

Une cellule est pas définition petite, et donc les vecteurs \vec{u_r},\vec{u_\theta},\vec{u_Z} sont constants et on fait donc le calcul comme en cartésiennes (voir le document fourni par vanoise p. 13). Ceci dans une cellule.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !