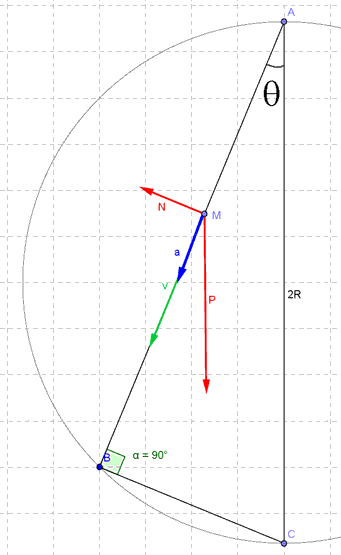
Je t'ai fait un schéma (sans tout y reporter). J'ai donc bien compris que A était le sommet du cercle, de diamètre 2R.

On appelle , l'angle que fait le segment [AB] avec la verticale.
De ce fait, tu as bien la relation suivante : AB = 2R.cos()

(Pour démontrer cela, il faut voir que ABC est un triangle rectangle en B car AC diamètre du cercle et B, point quelconque sur le cercle, cours de maths 4ème)


En fait, la résolution est la même que pour un plan incliné... On va donc se placer dans un repère mobile (Mxy) tel que (Mx) dirigé selon (AB) et (My), perpendiculairement (selon la réaction normale du fil ) avec pour origine du mouvement (temps et espace), le point A.


Maintenant, on applique la RFD :
P + N = m.a

Comme le mouvement s'effectue selon (AB), l'accélération est donc dirigée selon (AB) [résultante des forces], dans le sens de la vitesse car on conçoit bien que la perle "chute" donc accélère.

Ainsi, a = a_x = g.cos()

D'où v(t) = g.cos().t

Et enfin, la distance parcourue par la perle M, par intégration :
AM(t) = g.cos().t²/2


Lorsque le point mobile M atteint le point B après une durée t, la distance parcourue AB découle de l'équation horaire de ce mouvement :
AM(t) = g.cos().(t)²/2 = AB = 2R.cos()


On égalise les deux :
g.cos().(t)²/2 = 2R.cos()

D'où, après simplification, la valeur de t :
t = (4R/g)

t ne dépend que du rayon du cercle et de la valeur de la pesanteur, il ne dépend donc pas de la valeur de , et donc par conséquent de B.