bonjour de l'aide svp, Jai un exo que jai traité mais dont je doutes les reponses

On considère un élastique E de raideur k et de longueur au repos lo ainsi qu'une particule M de masse m.

1.    M étant accroché à E, déterminer l'allongement a de E ainsi que la pulsation ωo des oscillations verticales de M autour de sa position d'équilibre.
je trouve l'allongement a=mg/k et w₀=(k/m)
Mais pour l'allongement je sais pas si c'est l'allongement à l'équilibre ou bien c'est l'équation horaire z(t)
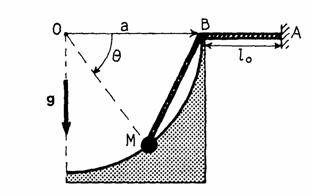
2.    On réalise un quart de circonférence de centre O et de rayon a. E, accroché en A, passe en B dans un petit anneau.  AB = l₀. M coulisse sans frottement sur le cercle. Établir l'équation différentielle du mouvement de M. Calculer α valeur de θ pour laquelle M est en équilibre. Étudier les petites oscillations de M au voisinage de cette position d'équilibre, calculer leur pulsation ω.
Pour établir l'équation différentielle est ce que je peux appliquer la RFD ici ? je voulais utiliser la conervation de l'énérgie mécanique et dériver cela pour trouver l'équation différentielle


Merci de bien vouloir m'aider