Inscription / Connexion Nouveau Sujet
Petit problème électrostatique
Bonsoir,
J'étudie depuis très peu l'électrostatique, or il y a quelque chose que je n'arrive pas à comprendre..
On a d'abord vu la charge Q puis ensuite le champ elec E.
La formule du champ elec étant : E=kQ/r² ac k=1/4
0
Pourquoi, dans un exercice des cosinus apparaissent ??
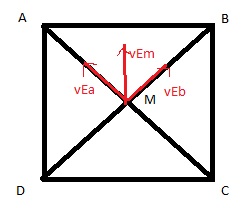
Exemple, un carré ABCD de côté a chargé à ses sommets tel que qa et qb <0 puis qc et qd > 0
=> Trouver la charge au centre du carré.
Résultat:
E(M)= 4
2KQ/a²
Je pense que le champ résultant est égale au champ E(A) + E(B) donc pourquoi pas : E(M)=2*KQ/(a2 /2)²
(AC diagonale =a2 )
Merci
bonsoir,
Oups !... Beaucoup d'imprécisions...
=> Trouver la charge au centre du carré.
Je suppose que c'est le champ électrique et non pas la charge.
D'autre part, les charges qA, qB, qC et qD sont-elles toutes égales en valeur absolue à Q ?
Le champ électrique au centre du carré est la somme vectorielle de 4 champs électriques.
Bonsoir!
Oui excuse moi c'est le champ électrique et non la charge qu'on cherche ici.
Enfaite, on me donne qA = qB = -Q et qC = qD = Q avec Q > 0
Donc vectE(M)= vectE(A)+ vectE(B) + vectE(C) + vectE(D)
or, vectE(B)=vectE(D) et vectE(A)=vectE(C)
Ainsi, vectE(M)= 2vectE(A)+2vectE(B) ?
Annuler
connectez vous