Inscription / Connexion Nouveau Sujet
Petit exercice Oscillateur Harmonique
Énoncé :
Une masse oscillante passe par sa position d'équilibre avec une vitesse dans le sens de l'axe des x à la date t1 = 1.44 ± 0.03s et elle passe ensuite pour la première fois à mi-distance entre la position d'équilibre et la position d'élongation maximum à la date t2 = 2.52±0.1s
- On prendra comme dans le cours X(t) = C * cos(ω0t + φ)
- On posera les équations qui permettent de déterminer ω0 et φ
- C ne peut être déterminé en l'absence d'info supplémentaire
1) Calculer la période des oscillations
Ma solution :
On a donc X(t) = C * cos(ω0t + φ)
j'ai compris que ω0t était la pulsation propre en s^-1 et φ la phase (sans unité) mais qu'est ce que cela représente pulsation et phase? Que représente C?
je ne comprends pas non plus quelles équations je dois poser pour déterminer ces deux valeurs
Pour trouver la période, on doit utiliser cette formule T = 2π/ω ..
2) Pourquoi n'a t-on pas choisi de mesurer l'instant où le mobile passe par la position d'élongation maximale?
Ma solution :
là je ne comprends pas du tout le sens de la question on a t1 = position d'équilibre (que représente t-elle?) et t2 = mi distance entre position d'équilibre et position d'élongation maximal après je ne comprend vraiment pas comment associer ces deux données avec la question
Merci pour votre aide!
Bonjour
En posant : , L'amplitude est C (constante positive) : c'est la valeur maximale que peut prendre x(t) au cours du mouvement ; la pulsation est
; la phase est
; la phase initiale est
. La période est la durée nécessaire pour que la phase augmente de
rad. Elle est donc reliée à la pulsation par la relation :
.
Ensuite, x=0 à la date t1 et x = C/2 à la date t2. Cela te donne un système de deux équations à deux inconnues :
Il faut aussi remarquer que la vitesse doit être positive à la fois à la date t1 et à la date t2. Cela conduit aux deux inégalités :
Petit oubli à mon message précédent : tu parles de phase "sans unité".
La phase correspond à un angle plan et, comme tu le constateras ici : ![]() , il faut utiliser le radian comme unité bien qu'il s'agisse d'une unité dérivée sans dimension physique.
, il faut utiliser le radian comme unité bien qu'il s'agisse d'une unité dérivée sans dimension physique.
La pulsation se mesure ainsi en rad/s.
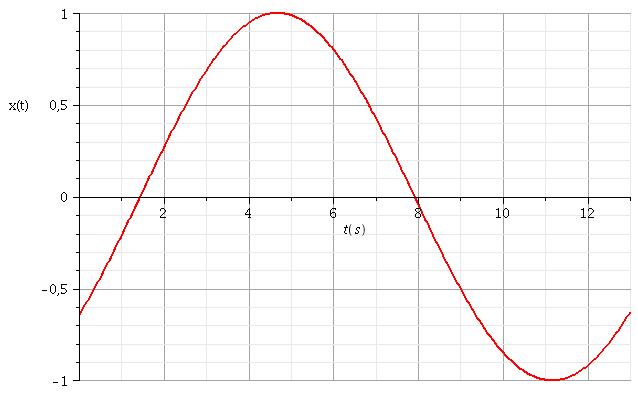
Pour mieux visualiser le mouvement, tu trouveras ci-dessous la courbe x=f(t) correspondant aux valeurs de  et
et  qu'il te faut déterminer. J'ai en revanche, choisi arbitrairement C = 1m.
qu'il te faut déterminer. J'ai en revanche, choisi arbitrairement C = 1m.