Inscription / Connexion Nouveau Sujet
Pesanteur apparente
Bonjour,
Voici l'énoncé d'un exercice dont j'ai du mal à arriver à la solution :
Un navire se déplace vers l'ouest, en suivant un parallèle, à la latitude , à la vitesse
.
Quelle est la variation relative du poids d'un corps associé à un tel mouvement, pour un passager du navire, qui utilise l'équilibre local d'un point matériel pour définir le poids d'un corps ?
Solution donnée : soit environ
soit environ
Je commence donc par utiliser la formule de changement de référentiel :
Avec le référentiel géocentrique, et
le référentiel terrestre non galiléen. Le corps se situe au point
.
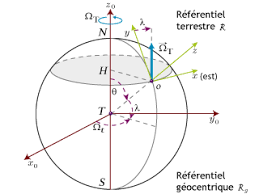
J'ai utilisé le repère joint en pièce-jointe.
Alors :
La vitesse du navire étant constante dans le référentiel terrestre, .
Le poids apparent correspond donc à
Avec H le projeté de M sur l'axe .
. Avec
le rayon terrestre.
Voici mon avancé pour le moment, mais pour être honnête, le de la solution me perturbe... je ne vois pas d'où il peut venir...
Pourriez-vous me dire si ce que j'ai fait pour l'instant est correct ?
Bonjour
Question préalable : que désignent et
dans ce problème ? Les vecteurs champ de pesanteur ou les vecteurs champ gravitationnel ? Probablement les vecteurs champ de pesanteur puisqu'il est question du poids de la personne. Or le vecteur poids est la somme de la force gravitationnelle et de la force d'inertie d'entraînement centrifuge due à la rotation de la terre autour de l'axe de ses pôles. Donc, si les vecteurs
et
désignent les vecteurs champ de pesanteur, tu n'as pas à faire intervenir le terme
qui est déjà inclus dans g.
En revanche tu dois faire intervenir la force d'inertie de Coriolis.
Le mouvement relatif par rapport à la terre est un mouvement circulaire uniforme de rayon r (rayon terrestre) puisque le personnage se déplace sur un méridien et décrit ainsi un arc de cercle.
Hum donc si je comprend bien :
Ensuite, honnêtement, je ne vois pas vraiment la démarche à suivre...
Pourriez-vous me dire quelle doit être la prochaine étape de calcul ?
Tu n'as pas compris mon message précédent. Tu confonds toujours vecteur champ de gravitation et vecteur champ de pesanteur.
Le vecteur champ de pesanteur est, en appelant "r" comme dans ton corrigé le rayon de la terre :
Le produit de par la projection de
sur la verticale locale est tout à fait négligeable devant
de sorte qu'il est possible, comme cela se fait usuellement, de considérer le vecteur
pratiquement vertical :
. Encore une fois : tu n'as pas à faire ce calcul puisque seule la variation relative de g est demandé.
Le poids apparent est la résultante du poids réel m.go, de la force d'inertie de Coriolis et de la force d'inertie centrifuge due au mouvement circulaire uniforme par rapport à la terre :
“v” est la vitesse du bateau par rapport à la terre. Reste à calculer la variation relative de g à la surface de l'eau, selon que le bateau est immobile ou en mouvement :
PS : tes notations ne sont pas toutes cohérentes entre elles et pas toujours en accord avec celles de la figure. J'ai dû un peu adapter... Ce que j'ai noté "g" semble être noté g' dans ton corrigé...
D'accord, j'ai compris vos calculs.
Néanmoins, je bloque toujours sur , d'où vient-il ?
Cela me fait penser à l'accélération normale, mais ici, est la vitesse du bateau par rapport au référentiel terrestre et non pas par rapport au référentiel géocentrique.
Pour rapport au référentiel terrestre, le passager se déplace le long d'un méridien à la vitesse v. Il est donc animé d'un mouvement circulaire uniforme de vitesse v et de rayon r (rayon terrestre). Dans ce cas, l'accélération par rapport à la terre est normale centripète de valeur v2/r . Revois au besoin ton cours sur le mouvement circulaire uniforme. Dans le référentiel lié au passager, on peut considérer que celui-ci est soumis à une force normale centrifuge de norme m.v2/r .
Petite erreur dans mon précédent message. Le déplacement se fait le long d'un parallèle, pas d'un méridien. "r" désigne donc le rayon de ce parallèle qui dépend du rayon terrestre et de la latitude.
En fait je suis d'accord avec vous, mais néanmoins, je ne vois pas comment apparaît ce terme dans le calcul.
Car n'apparaît pas dans l'accélération de Coriolis, ni dans
. Je dirais que ce terme vient de l'accélération d'inertie d'entrainement mais celle ci est comprise dans le champ de pesanteur ?
Je suis un peu perdu...
Le repère absolu supposé galiléen est le repère géocentrique.Le repère relatif est le repère lié au navire.
Deux rotations interviennent ici, ce qui génère deux forces d'inertie d'entraînement centrifuges :
1° : la rotation de la terre autour de l'axe de ses pôles. La force d'inertie d'entraînement correspondante n'est pas à étudier ici car elle est prise en compte dans le poids.
2° : la rotation du navire par rapport à la terre à la vitesse v le long d'un parallèle de rayon r. Cette force d'inertie centrifuge a pour intensité m.v2/r.
Cela conduit à mes calculs du 21-02-22 à 23:34.
D'accord, je pense avoir trouvé.
Ce terme apparaît dans . Ceci est bon, néanmoins, j'ai un autre petit problème qui apparaît :
si je prend en compte le mouvement circulaire du navire, alors je trouve :
Avec l'angle correspondant à la rotation uniforme du navire par rapport au centre de la terre.
Ainsi, j'ai du cosinus et du sinus dans l'expression de la force de Coriolis, puis-je m'en débarrasser ou bien faire des approximations ?
Au départ, j'avais considéré la vitesse selon , ce qui correspondrait à la solution donnée, mais serait-ce cohérent de faire cette approximation ?
La vitesse du navire par rapport à la terre a effectivement pour expression :
Cela n'est pas une approximation. Une grandeur vectorielle peut indifféremment être exprimée dans une base lié à R ou une base lié à R' et ici, le deuxième choix est largement plus simple tout en étant rigoureux.
D'accord, je pense avoir compris !!
En fait je n'arrivais pas bien à visualiser le repère terrestre et les différentes coordonnées. Je considérais le mouvement du navire par rapport au référentiel terrestre comme un mouvement de translation et non de rotation...
Le référentiel terrestre tourne par rapport au référentiel géocentrique.
Le navire tourne par rapport au référentiel terrestre.
Donc le navire est effectivement soumis à une accélération normale, à la force de coriolis et à son poids.
Néanmoins, prendre en compte la rotation du navire autour de la terre n'a que très peu d'influence non ? C'est d'ailleurs le but de l'exercice ? Car je pense à un exercice sur l'usure des rails de train où cette accélération normale n'était pas prise en compte.
D'accord avec ta conclusion : considérer le mouvement du navire comme circulaire plutôt que rectiligne apporte une correction sur g extrêmement petite, indétectable avec les appareils de mesures usuels.
J'ai une dernière petite question :
Je trouve donc
Avec le vecteur unitaire orienté suivant
avec H le projeté de M sur
.
Pour arriver à je fais donc une soustraction vectorielle ?
Puis je passe à la norme, et obtient donc le bon résultat.
Ma démarche est-elle correcte ?
Je pose beaucoup de questions mais j'aimerais vraiment avoir une démarche rigoureuse pour bien comprendre cet exercice !
Ce que tu as écrit est exact.
Je ne suis pas sûr que celui qui a rédigé le corrigé ait bien vu que le terme correctif n'est pas colinéaire au vecteur .
Il fournit un résultat valide rigoureusement seulement si le navire se déplace sur l'équateur.
Enfin l'essentiel, comme tu l'as déjà écrit, est de montrer que tenir compte des forces d'inertie dans ce contexte est sans intérêt.


