Inscription / Connexion Nouveau Sujet
perméabilité du sable
Bonsoir,
J'ai une question concernant le tp que je dois préparer pour la semaine prochaine dont voici l'énoncé :
Dans un milieu poreux vertical, l'axe Oz étant choisi ascendant, le débit volumique de fluide Q à travers une section S est donné par la loi de Darcy généralisée :
avec k la perméabilité du milieu, 
la viscosité dynamique du fluide et 
sa masse volumique.
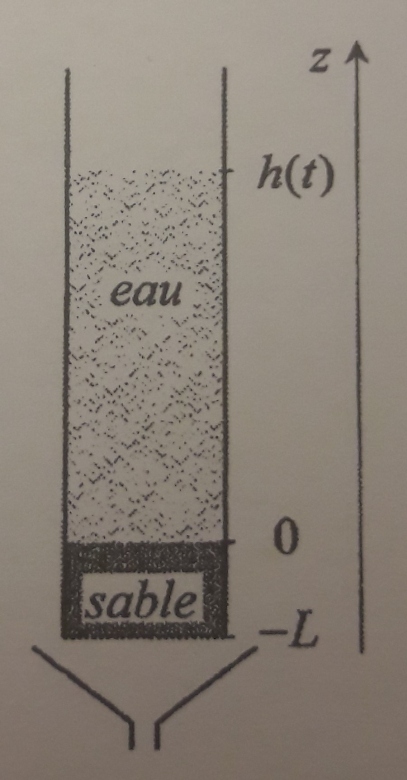
Montrer que l'évolution de la hauteur d'eau dans un perméamètre en fonction du temps suit une décroissance exponentielle.
Voici ce que j'ai fait :
On a car l'écoulement est unidimensionnel.
D'après l'équation fondamentale de la statique des fluides :
- entre -L et 0 : P(0)=Po-sablegL
- entre 0 et h(t) : P(0)=Po+eaugh
Il y a un indice dans l'énoncé qui dit que dP/dz doit être intégré sur l'ensemble du milieu poreux. Je vois bien que dP/dz est constant sur l'ensemble du milieu poreux puisque la variation de pression est nulle. Par contre je ne vois pas comment intégrer cela puisqu'on a deux masses volumiques différentes et que l'équation fondamentale de la statique des fluides est valable si on a une masse volumique constante.
Merci d'avance pour votre aide !
Bonjour
L'eau qui sort à la cote z=-L et celle à la surface libre à la cote z=h sont à la même pression : la pression atmosphérique. On peut donc écrire :
\int_{-L}^{0}\left(\frac{dP}{dz}\right).dz+\int_{0}^{h}\left(\frac{dP}{dz}\right).dz=0
A un instant donné, tu peux considérer je pense le débit volumique Q indépendant de z. La loi de Darcy devrait te permettre d'aboutir... Attention : il ne s'agit pas d'un problème de statique mais de dynamique des fluides.
Je ne comprends pas comment tu passes de :
L'eau qui sort à la cote z=-L et celle à la surface libre à la cote z=h sont à la même pression : la pression atmosphérique.
La variation élémentaire de pression entre l'altitude z et l'altitude (z+dz) peut s'écrire, dans le cas où la pression ne peut dépendre que de la variable de position z :
(propriété élémentaire des différentielles)
Cela conduit donc à :
Or la variation de pression atmosphérique sur une aussi faible variation d'altitude est totalement négligeable.
D'accord, merci. Mais ensuite je n'arrive pas à voir quelle est la primitive de dP/dz. Est-ce que c'est P ?
Autrement, dans un corrigé, il expliquait que dans l'eau la situation était proche de la statique des fluides mais pas dans le sable. Pourquoi ?
Pour l'intégration dans l'eau (entre z=0 et z=h), on peut négliger l'influence de la viscosité sur les parois du tube compte tenu de la très faible vitesse d'écoulement ; cela revient à utiliser la relation fondamentale de la statique des fluides :
par intégration :
On pourrait obtenir cette relation par le théorème de Bernoulli mais celui-ci n'est peut-être pas à ton programme.
Dans le sable, il faut utiliser la loi de Darcy :
Tu as tous les éléments en main maintenant...
Annuler
connectez vous