Inscription / Connexion Nouveau Sujet
Pendule élastique vertical
Bonjour
J'ai une question concernant cet exercice
La question 4
---
On considère un ressort à spires non jointives et constante de raideur et de masse négligeable suspendu à un support fixe. On suspend à l'extrémité libre du ressort un corps solide ( S ) de masse ( m ). On représente l'allongement du ressort à l'équilibre de ( S ) par ∆lo et on repère la position du centre d'inertie par un axe ( Oy ) orienté vers le haut dont l'origine coïncide avec la position du centre d'inertie de ( S ) à l'équilibre.
On écarte ( S ) verticalement de sa position d'équilibre vers le bas d'une distance d = 2 cm et on le libère sans vitesse initiale à instant t = 0 choisi comme origine du temps.
**Données :**
∆lo= 10,0cm
Intensité de pesanteur g=9,82m/s^2
1- Trouver, à l'équilibre, l'expression de K en fonction de m , g et ∆lo
2 - En appliquant la deuxième loi de Newton, établir que l'équation différentielle vérifiée par l'abscisse y
3 - La solution de cette équation s'écrit sous la forme :
y(t)=Ym.cos(3.pi/To +phi)
Déterminer la valeur de phi et To
4 - On note F la tension du ressort. Choisir la bonne réponse. Quand l'abscisse y > 0 :
a) F > mg
b) F = mg
c) F < mg
Justifier votre choix
---
merci d'avance
Bonjour
Tu écris l'allongement du ressort sous la lorme :
l-lo= lo+y
lo+y
Ensuite, la norme du vecteur force exercée par le ressort vaut :
F=k.(l-lo)
Que vaut k. lo ?
lo ?
Facile maintenant de conclure.
Dans mon message précédent, je n'ai répondu qu'à propos de la question 4. Si cela ne te paraît pas clair, commence par expliquer ici ce que tu as fait aux trois autres questions, histoire de vérifier que tu as bien compris les causes des oscillations.
Merci beaucoup Vanoise pour ta réaction.
Mais je pense que ∆l = ∆lo-y
L'axe oy est orienté vers le haut ( voir la figure)
- la condition d'équilibre est : K.∆lo=m.g
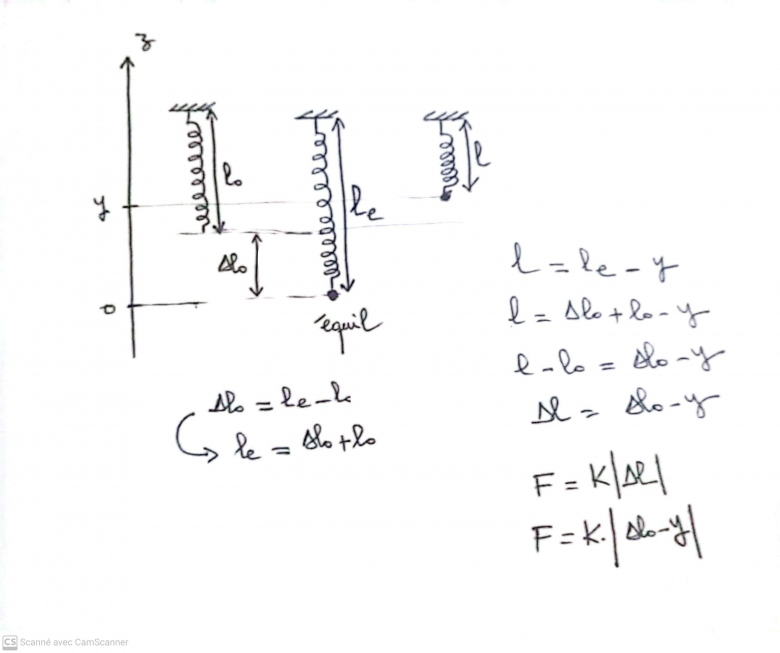
Étourderie de ma part : je n'avais pas vu que l'axe vertical est orienté vers le haut. Dans ces conditions, effectivement :
A l'équilibre :
en norme : P=F soit :
Dans le cas général :
En norme :
F=|P-k.y|
Je te laisse terminer. Tu as vu pas mal de choses ; tu as juste oublié de remplacer k. lo par P pour effectuer la comparaison.
lo par P pour effectuer la comparaison.
Cela n'est pas demandé mais, au niveau des sens des vecteurs, il est intéressant de remarquer que la résultante est toujours orientée vers la position d'équilibre correspondant au point O. Cette résultante constitue une force de rappel tendant en permanence à ramener le solide vers sa position d'équilibre.

 /To+
/To+ )
)

