Niveau maths spé

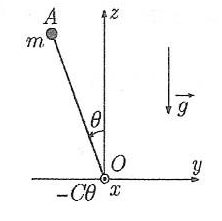
pendule de Holweck Lejay

Posté par
iSirrol 22-05-16 à 16:43

bonjour
pendule de Holweck Lejay
on a posé $\omega_0=\sqrt{\dfrac{C}{m\ell^2}}$ et $\gamma=\dfrac{mg\ell}{C}$

j'ai obtenu avec le théorème du moment cinétique : $\ddot{\theta}+\omega_0^2\theta=0$
j'ai obtenu avec la conservation de l'énergie mécanique : $\ddot{\theta}-\dfrac{g}{\ell}\sin\theta=0$
la combinaison des deux me donne : j'ai obtenu avec le théorème du moment cinétique : $\theta+\gamma\sin\theta=0$

on me demande la condition sur \gamma pour la $\theta=0$ soit une position stable, je ne vois pas comment la troisième équation m'indique quoi que ce soit à ce sujet, je n'ai donc pas du m'y prendre de la bonne façon

débloquez moi merci

Posté par re : pendule de Holweck Lejay 22-05-16 à 18:28

Bonjour
Tes deux relations sont fausses : tu ne tiens pas compte du couple de rappel exercée par le ressort. Vérifie aussi le signe de ton énergie potentielle de pesanteur. La méthode la plus efficace pour étudier les positions d'équilibre et la nature de celles-ci consiste à raisonner sur l'énergie potentielle : un équilibre correspond à un extremum de celle-ci ; s'il s'agit d'un maximum, l'équilibre est instable, s'il s'agit d'un minimum, l'équilibre est stable.
Tu dois démontrer que l'énergie potentielle élastique du ressort spiral vaut ½ C²
L'énergie potentielle totale est la somme de celle-ci et de celle de pesanteur. Tu devrais aboutir à montrer que deux cas sont possibles selon la valeur de :
1° Cas : un seul équilibre stable en =0 ;
2° Cas : un équilibre instable en =0 et deux équilibres stables en =_e (deux positions symétriques par rapport à (Oz))

Posté par re : pendule de Holweck Lejay 22-05-16 à 18:30

Je révise tout ca

Posté par re : pendule de Holweck Lejay 22-05-16 à 19:07

c'est vrai que l'une des questions nous invite à montrer qu'il existe une energie potentielle de ressort, mais en la faisant je ne l'avais pas compris comme cela .

on a $m\ell^2\ddot{\theta}+C\theta-mg\ell\sin\theta=0$
donc $m\ell^2\dot{\theta}\ddot{\theta}+C\dot{\theta}\theta-mg\ell\dot{\theta}\sin\theta=0$
et en intégrant $\frac{1}{2}m\ell^2\ddot{\theta}+\frac{1}{2}C\theta+mg\ell\cos\theta=E$

en introduisant $\gamma$ on a :
$\frac{1}{\omega_0}\ddot{\theta}+\theta-\gamma\sin\theta=0$

jusqu'à la tu es OK ?

Posté par re : pendule de Holweck Lejay 22-05-16 à 19:08

***EDIT COQUILLE***

$\frac{1}{\omega_0^2}\ddot{\theta}+\theta-\gamma\sin\theta=0$

Posté par re : pendule de Holweck Lejay 22-05-16 à 19:11

$\frac{1}{2}m\ell^2\dot{\theta}^2+\frac{1}{2}C\theta+mg\ell\cos\theta=E$
c'est mieux

Posté par re : pendule de Holweck Lejay 22-05-16 à 19:32

Une erreur à ta deuxième ligne : une primitive de .' est ½ C². Ce terme correspond à l'énergie potentielle élastique emmagasinée par le ressort spiral.
Si à l'expression de l'énergie mécanique, tu soustrait l'énergie cinétique, tu obtiens l'énergie potentielle :

$E_{p}=m\cdot g\cdot l\cdot\cos\left(\theta\right)+\frac{1}{2}C\theta^{2}$
Remarque : il n'était pas nécessaire de passer par l'énergie mécanique pour obtenir ce résultat... Il suffisait de partir de la puissance du couple exercé par le ressort pour obtenir ½ C². Quant à l'énergie potentielle de pesanteur...
Tu n'as plus qu'à étudier les variations de Ep en fonction de ... Je t'ai fourni quelques indications précédemment...

Posté par re : pendule de Holweck Lejay 22-05-16 à 19:53

oui c'est bon j'ai reussi à le faire

désolé pour toutes les coquilles j'avais le bon résultat sur feuille mais je l'ai mal recopié

merci

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

pendule de Holweck Lejay

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique