Inscription / Connexion Nouveau Sujet
Pendule d'Huygens
Bonjour,
je n'arrive pas à faire la question 1 de cette exercice, merci à tous ceux qui m'aideront, ^ ^:
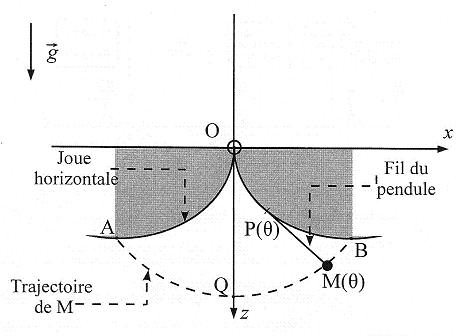
Enoncé: Afin de surmonter la non isochronie du pendule simple, Huygens a proposé la réalisation d'un pendule, avec un guide AOB("joues") sur lequel le fil s'enrole(cf imge suivante)
Le profil des joues est:
P(
) avec pour coordonnées:
xp()= R(2-sin(2)) et
zp()= R(1-cos(2)). Le point A est tel que =-
/2, B correspond à =/2 et O est le poin pour le lequel =0. Ce profil est cycloidale et l'equation paramétrique d'une clycloide est de ma nière génrale:
x(u)= R(2u-sin(2u)+x0 et
z(u)= R(1-cos(2u)+z0 l'axe Oz étant verticale orienté vers le bas. A et B sont les 2 points des joues où la tangente est horizontale donc dzp/dxp=0 en A ou B. A un instant donné, le fil du pendule est en contact avec la joue de O à P() puis libre de P() à M(). Le fil est tangent au profil de la joue en P().
1) Montrer que la paramètre qui définit la position du point P() vaut l'angle 
que fait vecteur P()M() avec la veticale.
2) Soit deux points de la jour P= P() et P'=P(+d). Donner l'expression du vecteur déplacement élémentaire dl qui permet de passer de P à P' et qui s'écrit dl= PP'=dxpux+dzpuz puis montrer que ||dl||= 4Rsin.d
Problème: pour la question 1 je ne sais pas du tout pas quoi commencé ="=""
On te dit que est tangent à la courbe de la cycloïde.
Ne peux-tu pas facilement trouver un vecteur tangent à cette même courbe (et donc colinéaire à ) à partir de l'équation de celle-ci?
Une fois ce vecteur trouvé, vérifie que le rapport de sa composante horizontale à sa composante verticale vaut .
Mais comment déterminer les coordonnées de M? Est ce qu'on doit reprendre l'équation paramétrique d'une cycloïde? Et en quoi déterminer pourquoi faut-l déterminer tan ?
Il n'y a pas besoin de déterminer les coordonnées de M.
On te donne
Est-ce qu'en calculant on n'obtiendrait pas un vecteur tangent à la courbe en P?
Il ne resterait alors plus qu'a déterminer l'angle formé par ce vecteur et la verticale.
on dérive seulement la 1ère composante c'est a dire qu'ona finalement:
dx(OP)=-2cos(2) mais après je ne comprend as ce qu'il faut faire....
et est ce que pour déterminer l'angle entre la verticale et la tangente on fait bien: dz/dx=2Rsin(2)/2R(1-cos()) (en reprenant le résultat précédent) on en déduit alors que dz/dx=1/sin(2)-sin(2)/cos()
Ta formule de dérivation est correcte, mais l'expression de la composante horizontale est . Il n'y a pas de raison que le premier terme disparaisse en dérivant.
Une fois la bonne expression obtenue, il faut utiliser les identités:
et
On en déduit directement que !
(Considère le triangle rectangle formé par les composantes horizontales et verticales du vecteur que l'on vient de calculer : ce vecteur fait un angle avec la verticale, le rapport de ses composantes vaut donc aussi
)
Ah ok, ^ ^ mais sinon on a dl=2R(1-cos(2).ux+2Rsin(2).uz
et après comment on en déduit que ||dl]]=4Rsin.d?
Après la question suivante c'est: 3) En déduire la longueur l() de la joue entre O et P(), et la longueur total la joue entre O et B, qui est la longueur du fil.
Pour l() on a l()= intégrale de dl-d (de =0 à /2) c'est bien cela?
(et on n'oublie pas ...)
Il suffit de développer et de regrouper de façon intelligente.
En suite, on a effectivement
avec la longueur du fil.
mais cet longueur du fil c'est bien la longueur du fil entre O et P() non? Comment à partir de cela on peut en déduire la longueur totale entre O et B?
mais il n'y avait donc aucune intérêt dans le sujet à ce qu'il demande la longueur l() de la joue entre O et P() puisque ces deux longueurs sont identiques
mais si j'ai bien compris, L= 
=0=/2dl.d et l()==0=dl c'est bien cela?
(La question suivante est: montrer que l'on peut exprimer en fonction de l() sous la forme: =arcos(1-(l/L)) est ce que pour cela on doit se servir de ||dl||?
Il faut bien sûr se servir de l'expression de pour déterminer l'expression de
.
donne, après intégration:
ou est une constante.
En remarquant que l(0)=0, on peut déterminer cette constante et ensuite arriver à l'expression qui t'es donnée.
Est ce qu'on avait bien l()==0 parce qu'après je trouve: arccos((-l+4R)/4R)=,cela est-il juste?(De plus que signifiait rmdl?)
(La question suivante est: Monterr que la position du point M()=
xm(=R(2+sin(2))
zm()=R(3+cos(2)) pour cela doit-on partir de PM=l-l())?
n'a aucun sens , on a montré que cet angle était égal à
donc on l'oublie...
On connait PM, on connait l'angle que forme le vecteur \vec{PM} avec la verticale. On a tout ce qu'il faut pour calculer la valeur de ses composantes.
Ensuite on écrite simplement
parce que si l(
)=L comment peut-on die alors que =arcos(1-l()/l)?!Mais d'où vient cette hypothèse farfelue?
Ah non, en faite c'est bon j'ai compris, ^ ^(je sais pas pourquoi mais je me suis mis dans la tête que =/2 ce qui n'est pas le cas).
Par contre je ne voit pas à quoi peut correspondre le vectru PM puisuq'on cherche déjà les coordonnée du vecteur M, peut-on dire que puisque PM et OP colinéaires alors PM=k OP(avec k appartient à 
)
Oui, on peut le dire si on a envie de torcher l'exercice! Bien sûr c'est complètement faux ... ^^
Si tu ne vois pas à quoi correspond , il y a un petit souci...
Tu comprends que composantes du vecteur ou coordonnées de M, c'est la même chose, n'est-ce pas?
Tu sais aussi que l'on peut décomposer en
?
On connaît depuis le début de l'exercice. Il ne reste donc qu'à calculer
. On connaît sa norme, on connaît son orientation donc c'est quasiment fini...
oui, je sais aussi qu'on peut décomposer OM en OP+OM et ||PM||=l-l()=4Rcos par contre je ne vois pas comment à partir de la orme on petue n déduire les coordoonée...="=(||AB]|=
(a²+b²) et pourquoi alors l'énoncé dit:"Grace à la détermination de on petu ensuite déterminer les coordonnées de M?
et pourquoi alors l'énoncé dit:"Grace à la détermination de on petu ensuite déterminer les coordonnées de M?
En ce qui me concerne, c'est une information nouvelle... Je te rappelle que tu es la seule personne à avoir l'énoncé complet sous les yeux.
Si un vecteur
non?
Annuler
connectez vous