Inscription / Connexion Nouveau Sujet
pendule amorti - frottements solides
Bonsoir,
J'ai une question à propos d'un TP où on considère les frottements solides d'un pendule amorti.
On considère que la force de frottements est toujours opposée à la vitesse et d'amplitude constante, de telle sorte que l'équation du mouvement du pendule s'écrit sous forme canonique (avec l'approximation des petits angles :
(
../wo²)+ = 
/ mgl = E si . >0 (dérivée de par rapport au temps)
(.. est la dérivée seconde par rapport au temps de ; est une constante positive égale au moment de la force de frottements sur l'axe de rotation du pendule (Ox) ; wo la pulsation propre du pendule.)
La question est: On lâche le pendule sans vitesse initiale à l'instant t = 0, depuis un angle > 0. Entre t = 0 et t = To/2 = 
/wo , quelle équation vérifie (t) ? Exprimez la solution (t) pour tout t compris entre 0 et To/2. Que vaut (t ) en t = t1 = To/2 ? Vous noterez 1 cette valeur.
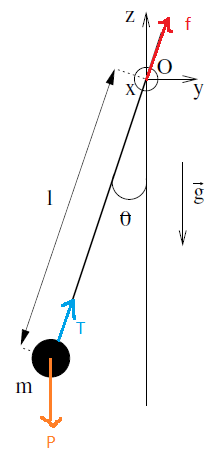
=> Je pense qu'il faut partir de la seconde loi de Newton, tels que ma = P + T + f , avec f la force de frottements, puis faire les projections sur les axes.
Seulement, je ne suis pas certaine d'avoir bien placé mon vecteur f, et je ne suis pas certaine de comprendre l'équation indiquée plus haut et ce qui est demandé dans la question. Dans le cas du pendule amorti l'énergie n'est pas constante mais je n'arrive pas à voir comment on peut obtenir cette équation et comment l'exploiter.
En remerciant d'avance ceux qui me répondront, je vous souhaite une bonne soirée.
Bonsoir tulipe70,
ton énoncé ainsi que le schéma soulèvent deux questions :
a/ la première est pour toi : tu dis " la force de frottements est toujours opposée à la vitesse", et tu la dessines dirigée de M vers 0 (M étant le point de masse m accroché au pendule). Cela voudrait dire que la vitesse de M serait dirige de O vers M, donc... que le fil du pendule s'allongerait, tout en restant dans la direction = cste ! Pas banal ça ! On n'est plus dans l'étude d'un solide qui oscille autour d'un point fixe 
.
a/ la deuxième est pour la personne qui a posé ce sujet : tu écris que la force de frottements est " toujours opposée à la vitesse et d'amplitude constante" : cela correspond bien à une force de frottement solide (confirmé par le titre de ton exercice), mais alors je voudrais bien savoir où se trouve le solide sur lequel M frotte et qui génère cette force f. Je ne connais qu'un exercice qui respecte les données de cet énoncé : le cas d'un solide qui se déplace en frottant à l'intérieur d'un hémisphère (par exemple, un glaçon dans un bol à déjeuner). Mais si c'est ça, que vient faire la tension T ?
Bref, avant de commencer une correction, j'aimerais que tu m'en dises un peu plus sur la nature du système physique à étudier.
Bonsoir prbebo,
tout d'abord je vous remercie pour votre réponse.
Lorsque vous indiquez " et tu la dessines dirigée de M vers 0 (M étant le point de masse m accroché au pendule). Cela voudrait dire que la vitesse de M serait dirige de O vers M " faite-vous référence au vecteur bleu ? Car ce dernier est la tension du fil T 
Le vecteur rouge est la force de frottements f, et je voulais donc savoir s'il était bien placé car je ne suis pas certaine.
Concernant le frottement solide, il s'agit du frottement de la tige (ou de sa base) sur l'axe fixe Ox. Il s'agit là d'un frottement solide, comme deux surfaces rugueuses l'une contre l'autre. Dans certains cas on considère la force de frottement de l'air (frottement visqueux) , ici c'est un frottement "dynamique" , comme on peut l'avoir avec la formule
f = 
c N, avec N la réaction normale du support et c le coefficient de frottement dynamique.
En effet, ce n'est pas la masse qui subit les frottements mais la tige.
f n'est évidemment pas bien dessiné.
Mais il faut aussi remarquer qu'on n'a aucun besoin de f pour répondre aux questions.
Le moment de la force de frottements sur l'axe de rotation du pendule (Ox) est donné est est suffisant pour répondre aux questions.
L'équation du mouvement est complaisamment fournie par l'énoncé, il suffit de la résoudre en tenant compte des conditions initiales ( et
)
Et ensuite calculer à partir de là, l'angle theta1 pour t = To/2
Sauf erreur, on arrive à (pas vérifié)
Attention aussi qu'on te dit qu'on part d'angle theta positif ... et que tu dessines avec un angle négatif (même si ce n'est pas fondamental dans la réflexion)
Sauf distraction.
Bonjour J-P,
Effectivement j'ai pu demander des précisions à mon enseignant, et la question n'était pas d'établir l'équation mais bien d'utiliser les deux données dans l'énoncé.
La première étant celle que j'ai écrite, et dans la seconde on a la même expression sauf que le frottement est négatif (pour Theta point < 0 )
Vous avez raison Merci pour toutes vos réponses !
Annuler
connectez vous