Inscription / Connexion Nouveau Sujet
Passe-bande - Régime impulsionnel
Bonjour
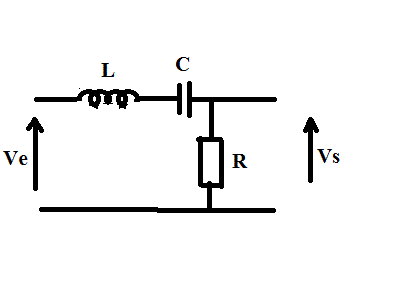
J'ai un circuit RLC série tension de sortie prise à la résistance
j'ai établit sa fonction de transfert en régime sinusoïdal
ma question est de trouver la relation entre la tension d'entrée et de sortie
(une équa diff) si l'entrée n'est pas forcément sinusoïdale
merci de m'aider si vous avez des idées
***Edit gbm : niveau changé en accord avec ta fiche de profil***
En sinusoïdal, tu as probablement des "jw" un peu partout.
Tu les remplaces par des (d.../dt) ... et c'est fait.
Par exemple (simple) si tu trouves en sinusoïdal : Vs/Ve = K(1 + jwT)/(1 + jw.A + j²w².B), alors on fait :
Vs.(1 + jw.A + j²w².B) = Ve.K(1 + jwT)
Vs + A.jw Vs + j²w².B.Vs = K.Ve + jwKT.Ve
on remplace jw par d.../dt et j²w² par d².../dt² ... et on arrive à :
Vs + A dVs/dt + B.d²Vs/dt² = K.Ve + K.T.dVe/dt
Attention de ne pas remplacer les j² par -1 dans la relation en sinusoïdal ... sous peine de louper les dérivées secondes dans l'équation différentielle cherchée par des signaux non sinusoïdaux.
Cette pratique n'est pas limitée à des équations du second ordre.
j^n.w^n sera remplacé par une dérivée n iéme ...
-----
Cette "pratique" est évidemment démontrable, mais ce n'est pas nécessaire dans les exercices concrets.
Sauf distraction.

Pour le moment les seuls choses que j'ai dit sont qu'
à basse fréquence :
à haute fréquence :
mais ces expressions sont issues de la première partie où l'on me demande à quelle condition le montage peut etre considéré comme pseudo-dérivateur ou pseudo-intégrateur.
rappel la fonction de transfert s'écrit (canoniquement) : avec les facteur de qualité et pulsation propre usuels
Même si cela va en remuer certains, mettre la fonction de transfert sous cette forme n'est pas des plus judicieux dans certaines (beaucoup) applications.
Il vaut souvent mieux laisser la fonction de transfert sous forme de pôles et zéros de forme (1 + jw.T) ou (1 + jw.A + j²w².B) ...
C'est idéal pour tracer par exemple les diagrammes de Bode ... mais aussi pour pouvoir facilement revenir à une équation différentielle dans le cas de signaux non sinusoïdaux.
*****
Quant à la forme canonique que tu donnes ..., ce n'en est qu'une parmi plusieurs autres.
Il y en a par exemple une autre ici :
![]()
Et une autre ici (au début) : ![]()
Chacune de ses formes a des avantages et des inconvénients.
Celle que tu donnes n'est pas la plus appropriée pour la question que tu as posée dans ton premier post.

Celle que tu donnes n'est pas la plus appropriée pour la question que tu as posée dans ton premier post.
je l'ai mise simplement à titre indicatif, d'ailleurs je ne savais même pas qu'on pouvait écrire des fonctions de transfert pour des régimes différents du sinuisoidal, tu viens de m'apprendre que c'était le cas ...
du coup sous une forme "plus polynomiale" j'ai :
ca ne m'aide pas tellement
***EDIT COQUILLE***
\dfrac{\mathrm d^2 s(t)}{\mathrm d t^2}+\frac{\omega _0}{Q}\dfrac{\mathrm d s(t)}{\mathrm d t}+\omega _0^2 s(t) =\frac{\omega _0}{Q}\dfrac{\mathrm d e(t)}{\mathrm d t}
On me dit que l'imprécision qui affecte \omega_0 (incertitude relative ) permet d'écrire la solution de l'équation homogène sous la forme
or quand je résoud l'équation caractéristique je trouve une solution qui s'écrit:
en posant j'ai effectivement le bon argument dans l'exponentielle
mais si je pose la pseudo pulsation je ne la retrouve pas en argument dans les fonctions trigo ...
ma question est donc qu'est ce qui me permet de dire que avec un raisonnement sur l'incertitude à priori (aux vues de la formulation de la question)
or quand je résoud l'équation caractéristique je trouve une solution qui s'écrit:
Je pense que c'est plutôt :

Faudrait voir l'ordre de grandeur de Q dans le problème.
Si Q > > 1/2, alors 4Q² > > 1 et
On aurait alors :
qui devient
soit
On aboutirait alors à :

merci
ta solution est la manière dont je l'avais fait mais la question est ambiguë puisque elle dit que c'est l'imprécision sur qui permet d'aboutir à cette écriture ... au final c'est plus simple
nouvelle question:
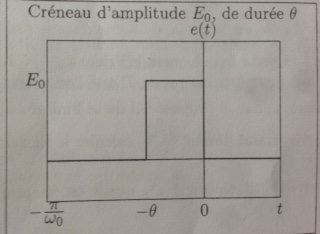
j'ai montré que était continu au moment
de la discontinuité de l'entrée et que
et j'aimerai connaitre l'expression de en fonction de
,
,
et
dans l'approximation de l'atténuation exponentielle négligeable (égale à 1)
Supposons Ve = 0 pour t < 0 et Ve = Eo pour t > 0 : (donc un échelon de tension epparaissant en t = 0)
Vs(t) = [A.cos(t * wo.RC(4Q²-1)/(2Q)) + B.sin(t * wo.RC(4Q²-1)/(2Q))].e^(-wo.t/(2Q)) + Eo (du moins si Q > 1/2)
Vs(0) = 0 --> A + Eo = 0, A = -Eo
Vs(t) = [-Eo.cos(t * wo.RC(4Q²-1)/(2Q)) + B.sin(t * wo.RC(4Q²-1)/(2Q))].e^(-wo.t/(2Q)) + Eo
(dVs/dt)(0) = 0 -->
-wo/(2Q) * (-Eo) + B.wo.RC(4Q²-1)/(2Q) = 0
Eo + B.RC(4Q²-1) = 0
B = -Eo/RC(4Q²-1)
Vs = [-Eo.cos(t * wo.RC(4Q²-1)/(2Q)) -Eo/RC(4Q²-1).sin(t * wo.RC(4Q²-1)/(2Q))].e^(-wo.t/(2Q)) + Eo
Vs = Eo.[1 - (cos(t * wo.RC(4Q²-1)/(2Q)) - 1/RC(4Q²-1).sin(t * wo.RC(4Q²-1)/(2Q))).e^(-wo.t/(2Q))]
Et si l'implusion est envoyée en t = -theta au lieu de t = 0, il suffit de décaler le résultat trouvé dans le temps
On aura alors :
Vs((t) = Eo.[1 - (cos((t + theta) * wo.RC(4Q²-1)/(2Q)) - 1/RC(4Q²-1).sin((t + theta) * wo.RC(4Q²-1)/(2Q))).e^(-wo.(t + theta)/(2Q))]
Et ceci pour t compris dans [-theta ; 0]
On peut alors calculer Vs(t) en t = 0
Et on peut aussi calculer I(t) en t = 0 (par I = C.dU/dt si j'en juge par le message du 22-10-15 à 22:58)
On obtient ainsi les conditions initiales à prendre en considération pour ce qui suit le flanc descendant de l'impulsion.
On repart alors de Vs(t) = [A'.cos(t * wo.RC(4Q²-1)/(2Q)) + B'.sin(t * wo.RC(4Q²-1)/(2Q))].e^(-wo.t/(2Q)) avec les conditions initiales qu'on vient de trouver (ce qui permet de calculer A' et B')
Et on a alors Vs(t) pour t > 0... dans le cas général (dont quel que soit theta)
Si on donne des conditions sur theta, on les introduit dans les résultats ... par exemple pour simplifier la relation trouvée.
Mais est-ce cela qui est attendu ?
-----
Rien vérifié. 
Vs(t) = [A.cos(t * wo.RC(4Q²-1)/(2Q)) + B.sin(t * wo.RC(4Q²-1)/(2Q))].e^(-wo.t/(2Q)) + Eo (du moins si Q > 1/2)
qu'est ce qui te permet d'écrire
d'autre part
(dVs/dt)(0) = 0 -->
qu'est ce qui te permet de dire ceci ?
la dérivée de la sortie n'est même pas continue en 0
j'ai démontré ceci
en plus de ces remarques j'ai indiqué que l'on négligeait l'atténuation exponentielle or tu la prends toujours en compte dans ta mise en équation.
Vs = (A.cos(Omega*t) + B.sin(Omega.t)).e^(-R.t/(2L))
Avec Omega la pseudo pulsation = ...
Supposons Ve = 0 en t = 0- (depuis "longtemps) et Ve = Eo en t = 0+
Vs(0) = 0 (car le courant dans le circuit est nul en t = 0 par la présence de l'inductance) ---> A = 0
Vs = B.sin(Omega.t) . e^(-R.t/(2L))
En t = 0+, Ve = Eo et avec Vs(0) = 0 eu Uc(0) = 0 --> UL(0) = Eo
Or UL = L.di/dt et comme Us = R.i --> UL = L/R * dVs/dt
UL(0) = L/R * (dVs/dt)(0)
Eo = L/R * B * Omega
B = Eo * R/(L*Omega)
Vs = Eo * R/(L*Omega) . sin(Omega.t) . e^(-R.t/(2L))
Si on est dans un cas tel que Omega presque égal Wo -->
Vs = Eo * R/(wo.L) . sin(wo.t) . e^(-R.t/(2L))
(dans laquelle on peut faire sauter R rt L et réintroduire Q)
valable de t = 0 à t = theta. (et sous réserve d'erreurrs)
Si l'implusion part en t = -theta alors, on décale dans le temps et on obtient :
Vs = Eo * R/(L*wo) . sin(wo.(t + theta)) . e^(-R.(t+theta)/(2L)) qui est valable de t = -theta jusque t = 0
Je suppose que si on néglige l'atténuation exponentielle c'est qu'on considère R.(theta)/(2L) comme quasi nul ...
On peut alors calculer Vs(0) = Eo * R/(L*wo) . sin(wo.theta)) ... qui servira comme condition intiale pour la réponse sur le flanc descendant de l'impulsion.
Il faudra aussi déterminer une 2eme conditions initiales ... (par exemple la valeur de Uc(0))
Attention, toujours rien relu. 
je suis désolé mais tu ne réponds pas à ma question en introduisant dans l'expression de la sortie
je cherche l'expression de en fonction de
,
,
et
EXCLUSIVEMENT dans l'approximation de l'atténuation exponentielle négligeable (égale à 1)
j'ai donc d'après ce qu'on a fait précedemment
ou encore sans approximation
avec
mais rien ne nous dit que l'approximation n'est plus valable donc
et la seule chose que l'on sache sur c'est
voilà où je suis bloqué merci de bien vouloir répondre à mes interrogations et/ou me signaler si j'ai fait une erreur plutôt que d'écrire une multitudes de lignes qui n'ont pas de rapport direct avec la question. [sans vouloir être offensant bien sûr car tout tes messages finissent pas un sourire]
Mais j'ai répondu.
On n'a pas s(t) = A.cos(wo.t) + B.sin(wo.t)
Mais bien s(t) = (A.cos(wo.t) + B.sin(wo.t)).e^(-Wo.t/(2Q))
Si le signal est Ve = 0 pour t < 0 et Ve = Eo pour t > 0 , alors :
Par la présence de l'inductance;, i(0) = 0 et donc Vs(0) = 0 ---> A = 0
s(t) = B.sin(wo.t) . e^(-Wo.t/(2Q))
En t = 0+, Ve = Eo et avec Vs(0) = 0 eu Uc(0) = 0 --> UL(0) = Eo
Or UL = L.di/dt et comme Us = R.i --> UL = L/R * dVs/dt
UL(0) = L/R * (ds/dt)(0)
Eo = L/R * B * wo
B = Eo * R/(wo.L)
Avec Q = wo*L/R
B = Eo/Q
--> s(t) = (Eo/Q).sin(wo.t) . e^(-Wo.t/(2Q))
Et si c'est en t = = -theta que l'impulsion de fait, alors on décale dans le temps et on obtient :
s(t) = (Eo/Q).sin(wo.(t+theta)) . e^(-Wo.(t+theta)/(2Q))
Et si l'atténuation exponentionnelle est néglgeable, je présume qu'on est sensé prendre e^(-Wo.(t+theta)/(2Q)) ^ratiquement égal à 1 et donc :
s(t) = (Eo/Q).sin(wo.(t+theta))
Qui répond à la question de la dernière ligne du message du 28-10-15 à 10:30
*****
Aux erreurs près bien entendu.

Fais-le plus tôt si tu veux ...
Attention que comme je l'ai dit dans un de mes messages, s(t) = (Eo/Q).sin(wo.(t+theta)) est valable pour t compris dans [-theta ; 0[
Pour trouver ce qui se passe pour t > 0, suite au flanc descendant de l'impulsion, il faut recommencer des calculs analogues en prenant cette fois comme conditions initiales, celles en t = 0
...

le que l'on considère est bien dans l'intervalle que du donne.
donc pas de soucis sur la mise en équation
bonjour
Or UL = L.di/dt et comme Us = R.i --> UL = L/R * dVs/dt
UL(0) = L/R * (dVs/dt)(0)
je comprend pourquoi tu fais ça et j'ai aussi envie de le faire
mais j'ai montré dans une question précédente que
ce qui est en contradiction avec
Eo = L/R * B * Omega
soit l'énoncé est incohérant soit on s'y prend mal pour trouver
soit l'énoncé est incohérant soit on s'y prend mal pour trouver B
Et bien je ne suis pas d'accord.
Le "B" que j'ai déterminé est celui valable sur ]-theta ; 0[
Donc valable jusqu'à l'instant ultime 0-
Il ne prend pas du tout en compte ce qui, pour lui sera fait dans "l'avenir" donc pour et au délà de t = 0+ (donc, entre autre, le flanc négatif de l'impulsion).
La relation
Je suis d'accord avec cette relation que je retrouve ainsi :
VL(0-) = -(Eo - s(0-) - Uc(0-))
VL(0+) = -(- s(0+) - Uc(0+))
Mais à cause de la présence de L --> s(0-) = s(0+) et comme la tension de C ne peut pas changer instantanémént, on a : Uc(0-) = Uc(0+)
On a donc :
VL(0-) = -(Eo - s(0-) - Uc(0-))
VL(0+) = -(- s(0-) - Uc(0-))
di/dt(0-) = -(Eo - s(0-) - Uc(0-))/L
di/dt(0+) = -(- s(0-) - Uc(0-))/L
Or s = R.i --> ds/dt = R di/dt -->
ds/dt(0-) = -(Eo - s(0-) - Uc(0-))*R/L
ds/dt(0+) = -(- s(0-) - Uc(0-))*R/L
ds/dt(0+) - ds/dt(0-) = Eo*R/L
ds/dt(0+) - ds/dt(0-) = (wo/Q)Eo ... on retrouve ta relation.
Mais elle n'a rien à voir avec le calcul du B pour t dans ]-theta ; 0[.
Pour trouver ce qui se passe pour t dans [0+ ; +oo[ il faut, comme je l'ai dit et répété, recommencer le même travail mais en repartant de nouvelles conditions initiales qui sont celles à l'instant t = 0-

merci pour ces infos claires
Pour trouver ce qui se passe pour t dans [0+ ; +oo[ il faut, comme je l'ai dit et répété, recommencer le même travail mais en repartant de nouvelles conditions initiales qui sont celles à l'instant t = 0-
ce n'est pas nécessaire de prendre