Inscription / Connexion Nouveau Sujet
particule sur un axe en rotation référentiel non galiléen
bonjour à tous
je suis en train de faire mon dm mais je bloque et je voulais avoir si vous pouviez m'aider?
un axe Ox tourne autour d'un axe vertical avec une vitesse angulaire w constante. l'angle entre Ox et l'axe verticale est notée 
une particule M de masse m coulisse sans frottement sur Ox
1 déterminer la position d'équilibre.Quelle est alors l'expression de la réaction R de l'axe sur M
ici j'ai utilisé le PFD en ajoutant la force d'entrainement sachant que coriolis est nulle car équilibre, j'ai donc
-mgcos+mxwsin2=0
x=(gcos)/(w2*sin2)
mais je ne vois pas du tout comment trouver R, on sait qu'il n'y a pas de frottement donc Rt est nulle, mais après je sèche
2 déterminer l'équilibre avec une méthode énergétique et déterminer sa stabilité
j'ai calculé le travail et donc est trouvé l'énergie potentielle : Ep=-0.5mw2x2
donc en est déduit l'énergie mécanique et j'ait dit que sa dérivée était nulle par rapport au temps (dEm)/dt=(0.5*m*2*x'*x")-0.5mw2x*x'*2)=0
voila et je ne sais pas trop quoi faire. Je me suis dit peut etre utilisé les moment cinétique mais je n'aboutit pas à grand chose avec ça...
si vous avez des idées ^^. merci d'avance
Bonsoir,
J'ai juste réfléchi à la première question. A partir de l'argument physique suivant je pense qu'il est possible de trouver R :
La masse soumise à son propre poids coulisse le long de l'axe incliné. Elle est donc accélérée RADIALEMENT vers l'axe vertical en raison du sinus de l'angle alpha.
L'axe incliné étant en rotation à vitesse angulaire constante w, la masse subit une accélération centrifuge bien connue. L'équilibre est atteint lorsque ces dernières se compensent.
m r w^2 = mg sin a
r = g sin a / w^2
1)
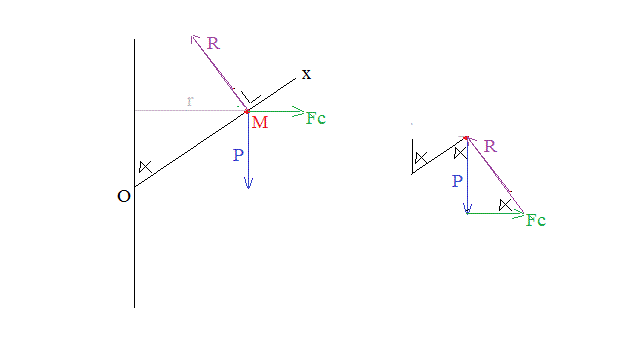
Soit r la distance de M à l'axe vertical
Force centrifuge sur M : Fc = mw².r
Poids de M = P = mg
La composée de Fc et P doit être perpendiculaire à OM pour que la particule reste en position sur l'axe OM.
--> P = Fc.tg(alpha)
mg = mw².r.tg(alpha)
r = g/(w².tg(alpha))
Et on a r = x.sin(alpha) ---> x = g/(w².tg(alpha).sin(alpha))
xM = g.cos(alpha)/(w².cos²(alpha)) (position d'équilibre de M sur l'axe Ox)
---
|R| = mg/sin(alpha)
Le vecteur R est perpendiculaire à OM vers le haut et dans le plan contenant l'axe vertical et d'axe OM.
-----
Sauf distraction. 
Salut,
Zut je me suis encore trompe, dans mon cas j'aurai du en fait avoir m r w^2 = mg tan a si je calcul correctement cette fois l'acceleration vers l'axe vertical mg tan a.. mais apparemment il faut aussi prendr en compte leffet de la reaction.. I see
merci beaucoup cela m'a bien aidé,
j'ai compris pour la position d'équilibre, mais je ne vois pas comment tu détermine R, utiliserai tu le PFD tu projettes l'accélération et tu en déduit les composantes de R, qui ne sont que des Rn mais il peut y en avoir selon x et l'axe verticale, comment en déduis tu que c'est perpendiculaire ? Et pour la méthode énergétique est ce que j'ai bien fait ?
merci encore ^^
Il ne peut pas y avoir de composante de la réaction du support (R) dans la direction de Ox. Une telle composante impliquerait qu'il existe du frottement entre la particule et le support Ox.
Mais l'énoncé précise que la particule coulisse SANS FROTTEMENT sur Ox.
Et donc R ne peut être que perpendiculaire à Ox.
A partir de là, tout est dit, à l'équilibre (par rapport à l'axe Ox) la somme vectorielle des forces P, R et Fc doit être nulle.
Et comme on connait P (en norme et en direction), en connaissant les directions de Fc(horizontale) et de R (perpendiculaire à OM), on peut calculer aussi bien R que Fc ...
ok merci beaucoup, et donc pour la méthode énergétique je fais comment ? comment on peut retrouver l'équilibre avec l'équation ?
Annuler
connectez vous