Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Paramètres admittances d'un dipôles.

Posté par
kamikaz 04-04-22 à 20:38

Bonsoir,

Merci d'avance.

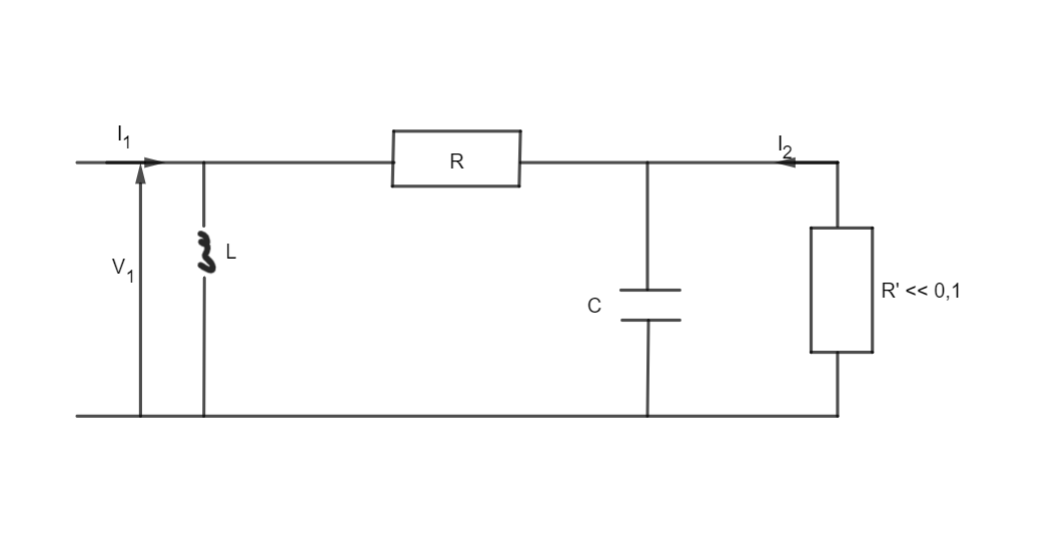
Déterminer les paramètres admittances du dipole suivant :

Paramètres admittances d\'un dipôles.

On a : \begin{cases} I_1 = Y_{11}V_1+ Y_{12}V_2 \\\ I_2 = Y_{21}V_1+ Y_{22}V_2   \end{cases}

\begin{bmatrix} I_1\\ I_2 \end{bmatrix} = \begin{bmatrix} Y_{11} & Y_{21} \\ Y_{12} & Y_{22} \end{bmatrix} \begin{bmatrix} V_1\\ V_{2} \end{bmatrix}

[Y] = \begin{bmatrix}Y_{11} & Y_{21} \\ Y_{12}&Y_{22}\end{bmatrix} est la matrice admittance contenant les paramètres admittances.

* On a : I_1 = Y_{11}V_1+ Y_{12}V_2

I_1 = Y_{11}V_1+ Y_{12}V_2

Y_{11} = \dfrac{I_1}{V_1}_{V_2 = 0}

Y_{12} = \dfrac{I_1}{V_2}_{V_1 = 0}

Y_{21} = \dfrac{I_2}{V_1}_{V_2 = 0}

Y_{22} = \dfrac{I_2}{V_2}_{V_1 = 0}

Posté par
vanoisere : Paramètres admittances d'un dipôles. 04-04-22 à 20:46

Pour chacun des quatre calculs, il faut faire un schéma équivalent du quadripôle dans les conditions de calculs.
Par exemples :
*  imposer une tension nulle revient à placer (en entrée ou en sortie selon le cas, un fil conducteur de résistance négligeable.
* imposer une intensité nulle en entrée revient à imaginer l'absence de générateur en entrée ; imposer une intensité de courant de sortie nulle revient à imaginer l'absence de dipôle branché en sortie.

Posté par
kamikazre : Paramètres admittances d'un dipôles. 04-04-22 à 21:07

Ok

Posté par
kamikazre : Paramètres admittances d'un dipôles. 04-04-22 à 22:44

Une question..

Est qu'on choisit arbitrairement la valeur de cette résistance négligeable ?

Posté par
kamikazre : Paramètres admittances d'un dipôles. 04-04-22 à 23:14

Par exemple pour le 1er Paramètres admittances d\'un dipôles.

çà va ?

Posté par
vanoisere : Paramètres admittances d'un dipôles. 05-04-22 à 18:56

Un éventuel courant d'intensité I2 venant du dipole branché en sortie du quadripole traverserait uniquement le court circuit pour ressortir. Il n'influence pas les paramètres d'entrée. On peut calculer Y11 comme si I2 =0. Donc, vu de l'entrée, le quadripole est équivalent dans ce cas particulier au dipole L//R. D'où l'expression de Y11.

Posté par
kamikazre : Paramètres admittances d'un dipôles. 05-04-22 à 21:22

J'ai pas compris..

Posté par
vanoisere : Paramètres admittances d'un dipôles. 05-04-22 à 22:36

À cause du court-circuit, aucun courant ne passe dans la branche contenant le condensateur. Tu peux donc le supprimer sans modifier la valeur de Y11.

Posté par
kamikazre : Paramètres admittances d'un dipôles. 05-04-22 à 23:10

Y_{11} = \dfrac{I_1}{V_1}_{V_2 = 0} = \dfrac{I_1}{I_1 Z_L + I_1 Z_R} = \dfrac{1}{Z_L + Z_R} = \dfrac{1}{jL\omega + R} = \dfrac{1}{jL\omega + R}  

Posté par
vanoisere : Paramètres admittances d'un dipôles. 06-04-22 à 16:48

R et L sont en parallèle et non en série !
Très simplement dans ce cas, les admittances complexes d'ajoutent pour obtenir l'admittance équivalente.

Posté par
kamikazre : Paramètres admittances d'un dipôles. 09-04-22 à 21:23

Ah oui, donc Y_{11} = \dfrac{1}{jL\omega} + \dfrac{1}{ R}

Posté par
vanoisere : Paramètres admittances d'un dipôles. 09-04-22 à 22:07

Oui !

Posté par
kamikazre : Paramètres admittances d'un dipôles. 09-04-22 à 22:14

Y_{22} = \dfrac{1}{jL\omega + \dfrac{1}{jC\omega}} + \dfrac{1}{R}

Posté par
kamikazre : Paramètres admittances d'un dipôles. 10-04-22 à 13:32

Oups..

À cause du court-circuit, aucun courant ne passe dans la branche contenant la bobine. Je peux donc la supprimer sans modifier la valeur de Y22.

Y_{22} = \dfrac{1}{ \dfrac{1}{jC\omega}} + \dfrac{1}{R} = jC\omega + \dfrac{1}{R}

Posté par
kamikazre : Paramètres admittances d'un dipôles. 10-04-22 à 17:18

Y_{12} = \dfrac{I_1}{V_2}_{V_1 = 0} = \dfrac{I_1}{I_1 Z_R + I_1 Z_C} = \dfrac{1}{ Z_R + Z_C} = \dfrac{1}{R + \dfrac{1}{jC\omega}}

Y_{21} = \dfrac{I_2}{V_1}_{V_2 = 0} =  \dfrac{I_1}{I_1 Z_R + I_1 Z_L} = \dfrac{1}{ Z_R + Z_L} = \dfrac{1}{R + jL\omega}

Posté par
vanoisere : Paramètres admittances d'un dipôles. 10-04-22 à 22:54

D'accord avec le message du 10-04-22 à 13:32 sur Y22.
Concernant Y12 et Y21 : on peut se contenter d'appliquer la loi d'Ohm à la résistance R. Dans chacun des deux cas, que vaut la différence de potentiel entre les deux bornes de R ?

Posté par
vanoisere : Paramètres admittances d'un dipôles. 11-04-22 à 18:47

Puisqu'il faut utiliser la loi des nœuds, il est sans doute plus rapide, pour ce genre de quadripôle en très simple, d'utiliser la loi des nœuds dès le début pour obtenir directement les quatre termes de la matrice admittance. YL,YR,YC désignent les admittances complexes des trois dipôles.

I_{1}=I_{R}+I_{L} avec : I_{R}=Y_{R}.\left(V_{1}-V_{2}\right) et : I_{L}=Y_{L}.V_{1}

I_{1}=\left(Y_{L}+Y_{R}\right).V_{1}-Y_{R}.V_{2}

Tu obtiens ainsi simplement Y11 et Y12.

I_{2}=I_{C}-I_{R}

I_{2}=-Y_{R}.V_{1}+\left(Y_{C}+Y_{R}\right).V_{2}

Tu obtiens ainsi Y21 et Y22 ; au final :

\left(\begin{array}{c} \\ I_{1}\\ \\ I_{2} \\ \end{array}\right)=\left(\begin{array}{cc} \\ Y_{L}+Y_{R} & -Y_{R}\\ \\ -Y_{R} & Y_{C}+Y_{R} \\ \end{array}\right)\left(\begin{array}{c} \\ V_{1}\\ \\ V_{2} \\ \end{array}\right)

Posté par
vanoisere : Paramètres admittances d'un dipôles. 11-04-22 à 18:49

J'ai oublié de reposter le schéma pour les sens d'orientations des courants.

Paramètres admittances d\'un dipôles.

Posté par
kamikazre : Paramètres admittances d'un dipôles. 11-04-22 à 23:04

Ok super

Merci beaucoup.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !