Inscription / Connexion Nouveau Sujet
panneau solaire et puissance
Bonjour, j'ai beaucoup de mal avec ce probleme, on cherche a trouver le nombre de panneau solaire qu'il faut pour alimenter plusieurs salles de cours.
voici l'enonce comportant le schema des classes et quelques documents concernant les panneau solaire.
***pdf migré sur le serveur : ![]() ***
***
pour la première salle je trouve trouver en reunissant toutes les résistances ( RL // ( R1//R2) + R3 + (R4// R6+R5)))
je calcule ensuite la valeur de chaque résistance avec la relation P=V^2/R donc R=V^2/P
RL=3,6
R1=3
R2=1,5 
R3=1
R4=4
R5=2
R6=2
et Req = 1,89 
en sommant toutes les puissances des chaque resistance j'ai une puissance nominale de 76 w et je trouve la meme valeur en utilisant seulement Req et les 12 V du generateur. a partir du graphe annexe 1 je trouve qu'un panneau solaire fourni environ 15W, il m'en faut donc 5 . Je ne trouve pas le point de fonctionnement du systeme.
Pour la deuxieme salle, je pense qu'il faut utiliser le theoreme de Kennely mais je sais seulement le faire pour passer de triangle vers etoile, j'ai beaucoup de mal pour l'autre sens qui est la transformation que l'on doit faire. J'ai en revance pu trouver la puissance nominale des toutes les lampes qui est de 108 w, il me faudrait donc 8 panneaux solaire.
j'ai encore plus de mal pour les deux autres salles.
merci
Bonsoir
Pour la salle 2 : la résistance centrale et les deux du haut constitue un "triangle" que tu peux remplacer par une "étoile". Il est alors facile de simplifier le montage.
Bonjour, oui c'est ce que j'ai essaye de faire avec le theoreme de Kennely mais je n'ai pas reussi. j'ai du mal a le faire dans ce sens.
Pour une généralisation plus aisée, je prends des notations « classiques ». A savoir : chaque résistance de l'étoile est égale au produit des deux résistances issues du même nœud divisé par la somme des trois résistances :
Pour gagner du temps pour mon schéma, j'ai représenté chaque résistance par un trait épais. Facile, à ton niveau, de trouver la résistance équivalente entre les bornes P et N.
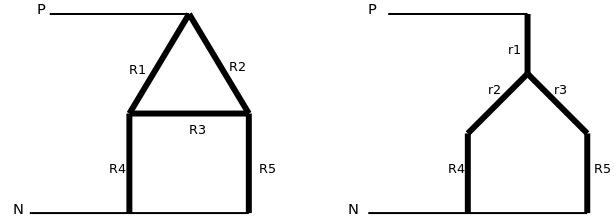
Bonsoir, en posant que r1 est en serie avec (R4+r2)//(r3+R5) je trouve
j'ai du mal pour la trois surtout avec le condensateur, il faut passer par les impedances complexes ?
merci
Tu as bien compris je pense malgré une etourderie dans la formule sur un indice.
Pour la salle 3 : en fonctionnement normal sous tension continue le condensateur est chargé sous 12V et n'intervient pas dans le bilan de puissance. En cas de microcoupure, tout se passe comme si les panneaux n'existent plus. Le condensateur se décharge alors à travers les résistances avec une constante de temps RC où R est la résistance équivalente aux lampes vues du condensateur. Sachant que la tension aux bornes de C passe de 12V à 11V en 100ms, facile de calculer C.


