Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

Oscillations, périodes, modes propres, pendules triples

Posté par
peppermint26 18-08-16 à 18:44

Bonjour,

Je dois étudier le cas de 2 pendules (masse au bout d'une tige), le premier est un ensemble de 3 pendules reliés entre eux par 2 ressorts (1 entre chaque) et le second un ensemble de 3 pendules reliés entre eux par 2 ressorts (1 entre chaque) et dont les pendules externes sont reliés au bâti par 1 ressort.

Pour ces deux cas, je n'arrive pas à trouver la pulsation propre de chacun des pendules afin d'avoir les périodes ainsi que de trouver les modes propres associés.

Ci-joint en image, les équations de mouvement des pendules du premier cas

la suite dans le poste suivant (besoin de mettre d'autres images)

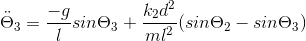
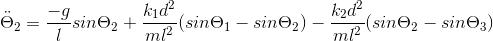
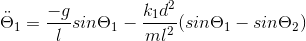
Oscillations, périodes, modes propres, pendules triples

Oscillations, périodes, modes propres, pendules triples

Oscillations, périodes, modes propres, pendules triples

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 18-08-16 à 18:46

Ci-joint, les équations de mouvement du second cas

Ici, l est la longueur du pendule
m, la masse
k, la raideur (malgrés les indices, tous les k sont identiques)
d, la distance à laquelle sont attachés les ressorts par rapport aux pivots
g, la gravité

Merci d'avance pour votre aide, je suis vraiment bloqué dans mon projet.

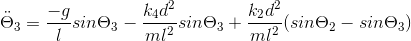
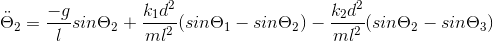
Oscillations, périodes, modes propres, pendules triples

Oscillations, périodes, modes propres, pendules triples

Oscillations, périodes, modes propres, pendules triples

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 18-08-16 à 20:03

Bonsoir
Je n'ai pas pris le temps (ou moins pour l'instant) de vérifier tes équations différentielles.
A priori, je pense qu'il faut :
1° : faire l'approximation des faibles amplitudes : tu l'as déjà faite plus ou moins implicitement en considérant que les ressorts restent horizontaux, ce qui revient à poser que les cosinus restent, au premier ordre près, égaux à 1. Très logiquement, tu dois considérer que les sinus sont, au premier ordre près, égaux aux angles exprimés en radians : \sin\left(\theta_{i}\right)\approx\theta_{i}
2° : remarquer qu'en régime sinusoïdal : \ddot{\theta_{i}}=-\omega^{2}\cdot\theta_{i}...

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 18-08-16 à 21:04

Bonsoir,

Merci pour votre réponse.
Oui, pour l'approximation du sin= je suis au courant et je le prend en compte, mais c'est pour trouver le 2 que je ne vois pas comment faire dans les équations où apparaissent plusieurs différents.

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 18-08-16 à 21:35


Je pose :

\omega_{0}=\sqrt{\frac{g}{l}}\quad;\quad\omega_{1}=\frac{d}{l}\sqrt{\frac{k_{1}}{m}}\quad;\quad\omega_{2}=\frac{d}{l}\sqrt{\frac{k_{2}}{m}}
En régime sinusoïdal, tes équations différentielles peuvent s'écrire sous forme matricielle :

\left(\begin{array}{ccc} \\ 0 & \omega_{2}^{2} & \left(\omega^{2}-\omega_{0}^{2}-\omega_{2}^{2}\right)\\ \\ \omega_{1}^{2} & \left(\omega^{2}-\omega_{0}^{2}-\omega_{1}^{2}-\omega_{2}^{2}\right) & \omega_{2}^{2}\\ \\ \left(\omega^{2}-\omega_{0}^{2}-\omega_{1}^{2}\right) & \omega_{1}^{2} & 0 \\ \end{array}\right)\cdot\left(\begin{array}{c} \\ \theta_{1}\\ \\ \theta_{2}\\ \\ \theta_{3} \\ \end{array}\right)=\left(\begin{array}{c} \\ 0\\ \\ 0\\ \\ 0 \\ \end{array}\right)
La condition sur pour que le système admette des solutions en i non nulles est très simple à comprendre (revois si nécessaire ton cours de math sur le sujet). En revanche, si tu considères les ressorts de raideurs différentes, le calcul est assez fastidieux, surtout dans le second cas...

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 18-08-16 à 22:34

Au temps pour moi : j'ai mal lu ton  message où tu précises que les ressorts sont identiques dans le second cas. Finalement : dans le premier cas, le calcul se simplifie beaucoup mieux que l'on pourrait le penser au départ...

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 18-08-16 à 22:49

Comment poses tu w0 , w1 et w2 ?
Sur un site que j'ai trouvé ils prennent \omega _{1}^{2}=\frac{g}{l}; \omega _{2}^{2}=\frac{g}{l}+\frac{k}{m};\omega _{3}^{2}=\frac{g}{l}+3\frac{k}{m}
Je ne comprend pas du tout comment on les choisis.
Pour les solutions en i, peux tu m'orienter sur le cours à revoir stp ?

Merci pour ton aide

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 18-08-16 à 23:30

Tu es en train de chercher la réponse sur internet au lieu de réfléchir à ce que j'ai écrit... Les trois pulsations que tu as trouvées sur internet sont justement les pulsations propres dans certains cas particuliers... Pas ici puisque, dans le premier cas : k1k2...
Mes trois notations ne sont pas a priori les pulsations propres. Ce sont trois notations qui simplifient l'écriture de tes équations différentielles. Tu n'as apparemment pas fait le lien entre les trois équations différentielles que tu as écrites et l'écriture matricielle de mon message de 21h39... La méthode pour résoudre ce problème suppose un minimum de connaissances sur les matrices et leurs déterminants...

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 11:09

Bonjour,

J'ai passé une grosse semaine à rechercher avant de poster sur ce forum, ce que je t'ai noté est le résultat de ces recherches. Etant donné que je n'ai pas compris comment y arriver, je me suis tourné vers ce forum pour avoir de l'aide.
Je me suis sans doute mal expliqué vu qu'il me fallait 2 postes pour écrire, dans les 2 cas tous les k sont égaux.
Pour le déterminant de la matrice je trouve :
+0-\omega ^{2}_{2}(0-\omega ^{2}_{2}(\omega ^{2}-\omega ^{2}_{0}-\omega ^{2}_{1}))+(\omega ^{2}-\omega ^{2}_{0}-\omega ^{2}_{2})((\omega ^{2}_{1})^{2}-(\omega ^{2}-\omega ^{2}_{0}-\omega ^{2}_{1})(\omega ^{2}-\omega ^{2}_{0}-\omega ^{2}_{1}-\omega ^{2}_{2}))

Qui en développant me donne :
-\omega ^{6}+\omega ^{6}_{0}-3\omega ^{4}_{0}\omega ^{2}+3\omega ^{4}\omega ^{2}_{0}+2\omega ^{4}\omega ^{2}_{1}+2\omega ^{4}\omega ^{2}_{2}-4\omega ^{2}\omega ^{2}_{0}\omega ^{2}_{1}-4\omega ^{2}\omega ^{2}_{0}\omega ^{2}_{2}-3\omega ^{2}\omega ^{2}_{1}\omega ^{2}_{2}+2\omega ^{4}_{0}\omega ^{2}_{1}+2\omega ^{4}_{0}\omega ^{2}_{2}+3\omega ^{2}_{0}\omega ^{2}_{1}\omega ^{2}_{2}


Etant donné que les ressorts sont egaux, \omega 1=\omega 2
donc :
-\omega ^{6}+\omega ^{6}_{0}-3\omega ^{4}_{0}\omega ^{2}+3\omega ^{4}\omega ^{2}_{0}+4\omega ^{4}\omega ^{2}_{2}-8\omega ^{2}\omega ^{2}_{0}\omega ^{2}_{2}-3\omega ^{2}\omega ^{4}_{2}+4\omega ^{4}_{0}\omega ^{2}_{2}+3\omega ^{2}_{0}\omega ^{4}_{2}

et si je remplace par leur valeurs :
-\omega ^{6}+\frac{g^{3}}{l^{3}}-3\frac{g^{2}}{l^{2}}\omega ^{2}+3\frac{g}{l}\omega ^{4}+4\frac{kd^{2}}{ml^{2}}\omega ^{4}-8\frac{gkd^{2}}{ml^{3}}\omega ^{2}-3\frac{k^{2}d^{4}}{m^{2}l^{4}}\omega ^{2}+4\frac{g^{2}kd^{2}}{ml^{4}}+3\frac{gk^{2}d^{4}}{m^{2}l^{5}}

Je ne vois pas trop quoi en faire.

Pour la matrice, quand je la développe, je ne retrouve pas mes équations différentiels.

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 12:00

Bonjour
Tu as effectivement bien travaillé !

Citation :
Pour la matrice, quand je la développe, je ne retrouve pas mes équations différentiels.

Logiquement si, à condition de prendre en compte qu'en régime sinusoïdal :
\ddot{\theta}=-\omega^{2}\cdot\theta
quel que soit l'indice donné à .
Ensuite, on démontre en math que, pour un tel système linéaire homogène, il existe des solutions autres que la solution triviale : \theta_{1}=\theta_{2}=\theta_{3}=0 seulement si le déterminant de la matrice des coefficients est nul. Cela te donne
effectivement une équation en de degré 6. J'obtiens le même résultat que toi.
Les exposants de l'inconnue étant tous pairs, cela te ramène à une équation de degré 3 d'inconnue 2.
Ensuite : imagine que les trois pendules oscillent en phase, les trois tiges restant constamment parallèles entre elles. Tout se passe dans ce cas particulier comme si les trois ressorts n'existent pas : chaque pendule oscille avec une pulsation égale à sa pulsation propre. 2=o2 est donc une racine de l'équation. Cela va te ramener à une équation de degré 2 que tu sais sûrement résoudre.
N'ayant pas bien compris s'il fallait considérer les ressorts identiques pour les deux situations ou seulement pour la seconde, je conserve, pour la première situation, 12.
Selon mes calculs, un peu fastidieux, les trois pulsations propres vérifient :

\boxed{\begin{cases} \\ \omega_{p1}^{2}=\omega_{0}^{2}\\ \\ \omega_{p2}^{2}=\omega_{0}^{2}+\omega_{1}^{2}+\omega_{2}^{2}+\sqrt{\omega_{1}^{4}+\omega_{2}^{4}-\omega_{1}^{2}\cdot\omega_{2}^{2}}\\ \\ \omega_{p3}^{2}=\omega_{0}^{2}+\omega_{1}^{2}+\omega_{2}^{2}-\sqrt{\omega_{1}^{4}+\omega_{2}^{4}-\omega_{1}^{2}\cdot\omega_{2}^{2}} \\ \end{cases}}

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 12:06

En supposant les ressorts identiques aussi dans le premier cas, la situation se simplifie fortement. Si en plus, on pose l=d, on obtient les résultats que tu as lu sur internet...

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 12:24

Au temps pour moi, je m'étais trompé entre les sur le développement. Je retrouve bien -\omega ^{2}\theta _{i}=\ddot{\theta }_{i}

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 12:25

Je regarde ça après mangé, merci
Les ressorts sont bien egaux, par contre ld

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 13:21

Je ne vois pas comment le degré de l'équation peut être de 3 et d'avoir pour inconnue 2. si je factorise par 2 alors j'aurais du 4 , 2 et si je factorise par 3 alors j'aurais du 3 , -3 , 1 , -1

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 14:13

Citation :
Je ne vois pas comment le degré de l'équation peut être de 3 et d'avoir pour inconnue 2

Si tu pose X=2, tu vas bien tomber sur une équation de degré 3.
Ensuite tu peux mettre en facteur (X-o2)  dans la mesure où X=o2 est une solution. Cela te ramène à une équation de degré 2...

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 16:27

Ah oui, je n'avais pas pensé au changement de variable, merci.
en posant X=2 , j'obtiens :
-X^{3}+3X^{2}\omega _{0}^{2}+4X^{2}\omega _{2}^{2}-3X\omega _{0}^{4}-8X\omega _{0}^{2}\omega _{2}^{2}-3X\omega _{2}^{4}+\omega _{0}^{6}+4\omega _{0}^{4}\omega _{2}^{2}+3\omega _{0}^{2}\omega _{2}^{4}

Ce qui me donne en factorisant pas X :
X(-X^{2}+3X\omega _{0}^{2}+4X\omega _{2}^{2}-3\omega _{0}^{4}-8\omega _{0}^{2}\omega _{2}^{2}-3\omega _{2}^{4}+\frac{\omega _{0}^{6}}{X}+\frac{4\omega _{0}^{4}\omega _{2}^{2}}{X}+\frac{3\omega _{0}^{2}\omega _{2}^{4}}{X})

Si je prend 02=2=X , j'obtiens 0.

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 18:00

Pour résoudre l'équation  du second degré, j'aurais fais le pour les 2 racines, mais il y a trois termes divisé par X.

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 19:51

Citation :
Si je prend X=o2 , j'obtiens 0.

Heureusement : il s'agit de la solution particulière que je t'ai justifiée physiquement tout à l'heure. La suite se traite comme en math, lorsque tu dois trouver les racines d'une équation de degré 3 alors qu'il y a une racine "évidente".
Il ne faut pas mettre en facteur X mais (X-02).

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 20:00

Aaaaaaah mais oui quel idiot --'
f(x)=(x-x1)(x-x2)(x-x3)
J'étais parti dans un calcul d'équation de degré 3 avec les méthodes de cardan et Tschirnhaus... C'est imbouffable comme calcul --'

du coup je dois faire (x-x1)(a'x2+b'x+c')=ax3+bx2+cx+d ?!

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 20:46

C'est une bonne méthode !

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 21:27

a'x^{3}+(b'+a'x_{1})x^{2}+(c'-b'x_{1})x-c'x1=ax^{3}+bx^{2}+cx+d
\begin{cases} & \text{ } a'=a \\ & \text{ } b'+a'x_{1}=b \\ & \text{ } c'-b'x_{1}= c \\ & \text{ } -c'x_{1}= d \end{cases}
\begin{cases} & \text{ } a'=a \\ & \text{ } b'=b-ax_{1} \\ & \text{ } c'= c+(b-ax_{1})x_{1} \end{cases}

je trouve mon determinant
\Delta =(b-ax_{1})^{2}-4a(c+(b-ax_{1})x_{1})

et les racines
x2=\frac{-b+ax_{1}-\sqrt{\Delta }}{2a} et x3=\frac{-b+ax_{1}+\sqrt{\Delta }}{2a}

qui me donne en remplaçant
x2=2\omega_{0}^{2}+2\omega _{2}^{2}+\frac{\sqrt{20\omega _{0}^{4}-6\omega _{2}^{4}+32\omega _{0}^{2}\omega _{2}^{2}}}{2}
et
x2=2\omega_{0}^{2}+2\omega _{2}^{2}-\frac{\sqrt{20\omega _{0}^{4}-6\omega _{2}^{4}+32\omega _{0}^{2}\omega _{2}^{2}}}{2}

Trouves tu la même chose ?

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 21:44

Je t'ai posté mes réponses dans mon message de 12h. Si tu les simplifies dans le cas de ressorts identiques, cela donne :

\boxed{\begin{cases} \\ \omega_{p1}^{2}=\omega_{0}^{2}=\frac{g}{l}\\ \\ \omega_{p2}^{2}=\omega_{0}^{2}+\omega_{1}^{2}+\omega_{2}^{2}+\sqrt{\omega_{1}^{4}+\omega_{2}^{4}-\omega_{1}^{2}\cdot\omega_{2}^{2}}=\omega_{0}^{2}+3\omega_{1}^{2}=\frac{g}{l}+3\frac{d^{2}}{l^{2}}\frac{k}{m}\\ \\ \omega_{p3}^{2}=\omega_{0}^{2}+\omega_{1}^{2}+\omega_{2}^{2}-\sqrt{\omega_{1}^{4}+\omega_{2}^{4}-\omega_{1}^{2}\cdot\omega_{2}^{2}}=\omega_{0}^{2}+\omega_{1}^{2}=\frac{g}{l}+\frac{d^{2}}{l^{2}}\frac{k}{m} \\ \end{cases}}
Dans le cas particulier d = l, cela donne les réponses que tu as trouvées sur internet...

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 21:57

Je ne comprend pas pourquoi j'en suis aussi loin...
Au niveau du déterminant as tu la même formule que moi ?

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 22:06

Si cela peut t'aider : en posant toujours 2=X, l'expression du déterminant peut s'écrire :

\left(X-\omega_{0}^{2}\right)\left[-X^{2}+X\left(2\omega_{0}^{2}+4\omega_{1}^{2}\right)-\left(\omega_{0}^{4}+4\omega_{0}^{2}\omega_{1}^{2}+3\omega_{1}^{4}\right)\right]

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 22:24

La formule que tu as postée hier soir à 23h30 me semble correcte.

-\omega ^{6}+\omega ^{6}_{0}-3\omega ^{4}_{0}\omega ^{2}+3\omega ^{4}\omega ^{2}_{0}+4\omega ^{4}\omega ^{2}_{2}-8\omega ^{2}\omega ^{2}_{0}\omega ^{2}_{2}-3\omega ^{2}\omega ^{4}_{2}+4\omega ^{4}_{0}\omega ^{2}_{2}+3\omega ^{2}_{0}\omega ^{4}_{2}
J'ai conservé l'indice 1 et toi l'indice 2 mais cela ne change évidemment rien au problème.

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 23:06

je viens de faire le développement et je tombe sur la même chose, je ne sais pas du tout comment tu as factorisé par x-02 mais ça fonctionne ^^'

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 19-08-16 à 23:31

alleluia je trouve les même racines ! Merci beaucoup !

Grace à ces pulsations, je peux trouver mes période T=\frac{2\pi }{\omega _{i}}

Par contre pour trouver les modes propres, je ne vois pas vraiment comment procéder...

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 20-08-16 à 10:53

Bonjour
Je t'ai déjà décrit physiquement le plus simple des modes propres afin d'obtenir sans calcul la racine =o.
Mathématiquement : si tu remplaces par p1=o dans la matrice des coefficients ou dans tes équations différentielles, tu vas constater que les solutions sinusoïdales correspondent à 1=2=3 t. Le premier mode propre correspond à :

\theta_{1}=\theta_{2}=\theta_{3}=A\cdot\cos\left(\omega_{0}t+\varphi_{0}\right) où A et o sont deux constantes.
Comme déjà dit : dans ce cas particulier, les trois pendules oscillent en restant constamment parallèles entre eux : les ressorts n'interviennent pas !
Ensuite remplace par p2 : tu obtiendras une autre relation entre les trois angles et un second mode propre.... idem pour =p2.
La solution générale est une combinaison linéaire des trois modes propres... Tu vas faire intervenir dans le cas général 6 inconnues. Les conditions initiales te fournissent 3 conditions sur les valeurs des angles et trois conditions sur les valeurs des vitesses angulaires ; le compte est bon !

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 20-08-16 à 11:36

Evidemment, dans mon message précédent, il faut lire :
Ensuite remplace par p2 : tu obtiendras une autre relation entre les trois angles et un second mode propre.... idem pour =p3.

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 20-08-16 à 21:14

Bonsoir Vanoise,

J'ai réussi à calculer les modes propres pour mes 2 cas. Pour le second, étant donné qu'il n'y avait pas de racine évidente, j'ai utilisé le logiciel Xcas pour avoir les racines.

Merci beaucoup pour ton aide !

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 20-08-16 à 22:03


Voici les résultats que j'ai obtenus pour les deux modes propres non encore traités ici.
Dans le cas : \omega_{p2}^{2}=\omega_{0}^{2}+3\omega_{1}^{2}, le fait de remplacer dans les équations différentielles 2 par p22 conduit aux équations , écrites sous forme matricielle :

\left(\begin{array}{ccc} \\ 0 & \omega_{1}^{2} & 2\omega_{1}^{2}\\ \\ \omega_{1}^{2} & \omega_{1}^{2} & \omega_{1}^{2}\\ \\ 2\omega_{1}^{2} & \omega_{1}^{2} & 0 \\ \end{array}\right)\cdot\left(\begin{array}{c} \\ \theta_{1}\\ \\ \theta_{2}\\ \\ \theta_{2} \\ \end{array}\right)=\left(\begin{array}{c} \\ 0\\ \\ 0\\ \\ 0 \\ \end{array}\right)
Facile de montrer que ce système correspond à :

\theta_{1}=-\frac{\theta_{2}}{2}=\theta_{3}=B\cdot\cos\left(\omega_{p2}t+\varphi_{2}\right)
Ce mode propre peut être obtenu, par exemple, en écartant vers la droite les pendules 1 et 3 du même angle, en écartant vers la gauche le pendule 2 d'un angle double et en abandonnant le système sans vitesse initiale.
Dans le cas : \omega_{p3}^{2}=\omega_{0}^{2}+\omega_{1}^{2}, le fait de remplacer dans les équations différentielles 2 par p32 conduit aux équations , écrites sous forme matricielle :

\left(\begin{array}{ccc} \\ 0 & \omega_{1}^{2} & 0\\ \\ \omega_{1}^{2} & \omega_{1}^{2} & \omega_{1}^{2}\\ \\ 0 & \omega_{1}^{2} & 0 \\ \end{array}\right)\cdot\left(\begin{array}{c} \\ \theta_{1}\\ \\ \theta_{2}\\ \\ \theta_{2} \\ \end{array}\right)=\left(\begin{array}{c} \\ 0\\ \\ 0\\ \\ 0 \\ \end{array}\right)
Il est facile alors de montrer que ce système correspond à :

\theta_{1}=-\theta_{3}=C\cdot\cos\left(\omega_{p3}t+\varphi_{3}\right)\quad et\quad\theta_{2}=0\;\forall t
Le pendule 2 reste immobile, les pendules 1 et 3 oscillent en occupant à chaque instant des positions symétriques par rapport au pendule 2. Ce mode peut être obtenu (par exemple) en écartant le pendule 1 d'un certain angle vers la gauche, le pendule 3 du même angle vers la droite et en abandonnant le système sans vitesse initiale.
Comme déjà dit, le cas le plus général correspond à une combinaison linéaire de ces trois cas particuliers.

Citation :
Citation :
Pour le second, étant donné qu'il n'y avait pas de racine évidente, j'ai utilisé le logiciel Xcas pour avoir les racines.

Courage ! Le système n° 2, a priori plus compliqué à cause des deux ressorts supplémentaires, se révèle plus simple à traiter mathématiquement : racine évidente pour la recherche des pulsations propres... Voici le système d'équations différentielles écrit sous forme matricielle :

\left(\begin{array}{ccc} \\ 0 & \omega_{1}^{2} & \left(\omega^{2}-\omega_{0}^{2}-2\omega_{1}^{2}\right)\\ \\ \omega_{1}^{2} & \left(\omega^{2}-\omega_{0}^{2}-2\omega_{1}^{2}\right) & \omega_{1}^{2}\\ \\ \left(\omega^{2}-\omega_{0}^{2}-2\omega_{1}^{2}\right) & \omega_{1}^{2} & 0 \\ \end{array}\right)\cdot\left(\begin{array}{c} \\ \theta_{1}\\ \\ \theta_{2}\\ \\ \theta_{3} \\ \end{array}\right)=\left(\begin{array}{c} \\ 0\\ \\ 0\\ \\ 0 \\ \end{array}\right)
Observe bien les termes de la matrice des coefficients : la seconde diagonale contient trois termes identiques, la première diagonale contient deux "0". Il est évident dans ce cas que le terme commun va pouvoir rester en facteur : surtout ne pas développer ! Tu as donc une pulsation propre "évidente" vérifiant :

\omega_{p1}^{2}=\omega_{0}^{2}+2\omega_{1}^{2}

La suite se traite comme le cas n° 1...

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 10:59

Bonjour Vanoise, j'ai oublié une dernière question,

Pour les 2 autres modes, je trouve la même chose que toi.

Les périodes que je trouve sont pour les modes propres. Mais si je donne un angle à un seul pendule, quelle sera la période de chaque pendule ?

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 11:10

Bonjour

Citation :
Mais si je donne un angle à un seul pendule, quelle sera la période de chaque pendule ?

Chaque équation(t) sera une somme de 3 fonctions sinusoïdales de pulsations égales aux trois pulsations propres. Comme ces pulsations ne sont pas, en règle générale, multiples les unes des autres, on ne peut pas définir une période. Si les pulsations propres sont numériquement proches, on observe en général un phénonmène de battement. Si tu veux, poste ici les valeurs numériques des pulsations propres et un exemple de conditions initiales. Nous traiterons le problème ensemble.

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 11:29

k=3
d=0,2
g=8.81
l=0,4
m=

Pour le premier cas avec un angle de 10° sur 1 , j'obtiens :

Oscillations, périodes, modes propres, pendules triples

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 11:36

et m=0.88

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 11:43

OK ! Tu obtiens effectivement un phénomène de battement.

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 11:45

En restant dans les petites déformations oui.

Mais du coup, je ne vois pas vraiment comment trouver la période de chaque pendule.

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 11:58

Je trouve donc pour mes periodes propres :
\omega _{p1}\simeq 4.95
\omega _{p2}\simeq 4.57
\omega _{p3}\simeq 7.92

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 15:27

Tu n'as pas bien compris mon message de 11h10.
Suppose que tu ais, par exemple : p3=4p1 et p2=3p1. Chaque élongation angulaire serait la somme de 3 fonctions sinusoïdales de fréquences multiples les unes des autres. Le théorème de Fourier permet alors d'affirmer que chaque pendule oscille à la fréquence la plus petite (dite  fondamentale) f_{1p}=\frac{\omega_{1p}}{2\pi}. Ici les trois périodes T1p, T2p, T3psont assez proches les unes des autres. La période T est la plus petite valeur positive telle que (t+T)=(t) t. C'est donc la plus petite valeur vérifiant :
T=n.Tp1=p.Tp2=q.Tp3 où n,p,q sont trois entiers positifs.
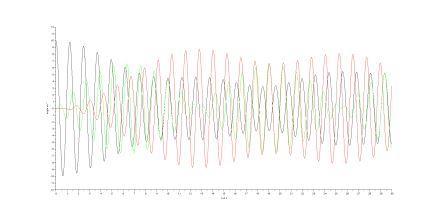
Compte tenus des valeurs assez proches des trois périodes propres, cette valeur théorique T est tellement grande qu'en pratique, on considère que les pendules n'oscillent pas de façon périodique : leurs mouvements sont amortis sur des durées bien inférieures à cette valeur théorique T. Tu peux observer tes courbes pour t'en convaincre.
Pour tes valeurs numériques : je suppose qu'il s'agit des pulsations propres :
n'oublie pas les unités ; comment peux-tu trouver p2<p1 ??
Je n'ai pas le temps maintenant de vérifier tes courbes. Je le ferai ce soir...

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 15:46

oui, je me suis trompé, ce sont les pulsations et non les périodes et elles sont en rad/s.\omega _{p1}=\sqrt{\frac{g}{l}}
\omega _{p2}=\sqrt{\frac{g}{l}}+\sqrt{\frac{kd^{2}}{ml^{2}}}
\omega _{p3}=\sqrt{\frac{g}{l}}+\sqrt{\frac{3kd^{2}}{ml^{2}}}
donc \omega _{p1}=\omega _{p2}

Pour les courbes, j'utilise le module Xcos de scilab, en rentrant mon système, j'affiche ces courbes pour 1 = 10°

Je ne vois pas comment je peux poser p2 et p3 en fonction de p1 puisque p2 et p3 sont égaux à p1 + \sqrt{\frac{xkd²}{ml²}}
ou x = 1 pour p2 et x=3 pour p3

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 19:11

Tu n'as pas compris mon message : c'est justement parce qu'il n'existe pas de relation simples telles que , par exemple : p3=4p1 et p2=3p1 ni, plus généralement de relation telle que : n.Tp1=p.Tp2=q.Tp3 où n,p,q sont trois entiers positifs qu'il est impossible de définir une période d'oscillation pour chaque pendule...

Posté par
peppermint26re : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 19:29

D'accords, donc c'est impossible.
Non désolé, je n'avais pas compris ça dans ce sens.
Merci

Posté par
vanoisere : Oscillations, périodes, modes propres, pendules triples 21-08-16 à 19:57

Citation :
Non désolé, je n'avais pas compris ça dans ce sens.

Pas grave ! Ce problème est intéressant mais pas simple !
Je trouve excellent qu'un élève ingénieur sache utiliser SCILAB ou MATLAB. Cependant, ici, écrire les équations horaires (t) pour chaque pendule pourrait t'aider à mieux comprendre ce qui se passe.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !