pour l'énergie,erreur de frappe

Bonsoir
Pour un mouvement rectiligne,
F=-dEp/dx
Plus généralement  : passer par le gradient si cela est à ton programme.

Petite interrogation : dans la mesure où le titre parle de puits de potentiel, l'expression de l'énergie potentielle ne serait pas plutôt :


?

Bonjour,

Oui,il manque bien un - pardon.Nous n'avons pas vu l'opérateur gradient,seulement évoqué.Dans votre réponse vous dites que F=-dEp/dx pour un mouvement rectiligne mais rien n'évoque un mouvement rectiligne dans la consigne. Et puis F=-dEp/dx n'est-il pas seulement valable pour une force conservative ?

Encore merci de votre réponse !

Dans le cas d'une étude en 3D, il faudrait utiliser la formule du gradient que je t'ai fournie. Ici, l'énergie potentielle ne dépend que de x. Si tu projettes la formule du gradient dans un repère (O,x,y,z), tu vas remarquer que seule la composante de la force suivant x est non identiquement nulle et s'écrit F=-dEp/dx . Partant d'une situation de vitesse initiale nulle, une telle force ne peut provoquer un mouvement que suivant l'axe des x.
A partir du moment où une énergie potentielle peut être définie, la particule est nécessairement soumise à la force F dont on vient de fournir les caractéristiques. La particule est-elles soumises à d'autres forces qui ne seraient pas conservatives, des forces de frottement par exemple ? Si l'énoncé n'évoque pas cette existence, on peut supposer raisonnablement que non.
Très vraisemblablement, il s'agit dans ce problème d'étudier le mouvement rectiligne d'oscillation de la particule autour de la position x=0 qui correspond au minimum d'énergie potentielle donc à la position d'équilibre stable de la particule.
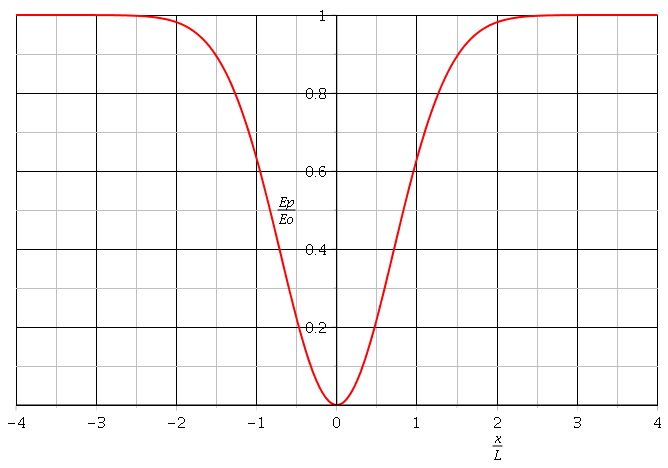
Cela t'aidera peut-être : voici une représentation de Ep en fonction de x. N'ayant pas de valeurs numériques, j'ai représenté en fait les variations de Ep/Eo en fonction de x/L.
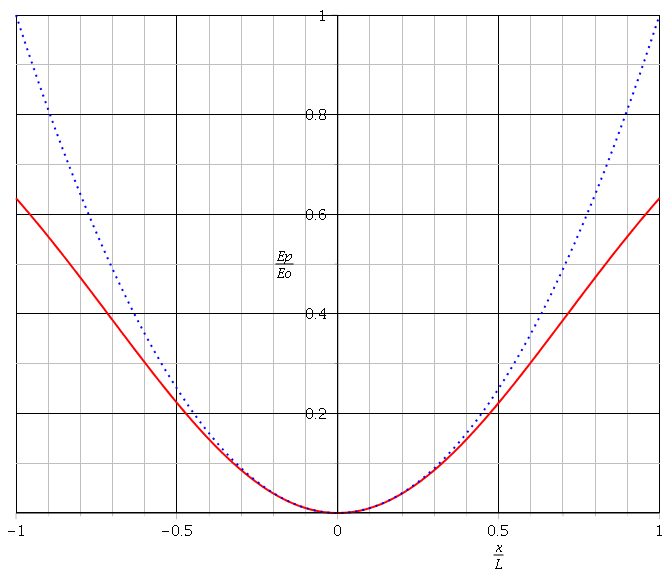
Le second graphe présente un effet de zoom de la première au voisinage du fond du puit, pour |x/L|<1. On peut remarquer que pour |x/L|très faible (inférieur à 0,5 environ) la courbe est assimilable à une parabole (tracée en pointillés bleus) . Pour |x| petit devant L, on peut écrire Ep½k.x²...

Bonjour,

merci beaucoup de votre réponse si détaillée,c'est beaucoup plus claire maintenant.
Il est spécifié que les frottements sont négligeables.On peut donc en déduire par le PFD que son équation de mouvement,projeté sur l'axe ex est : puis juste les calculs à finaliser et à simplifier tous ce qui est possible ?

C'est bien cela l'équation différentielle du mouvement. Dans le cas général, tu vas obtenir une équation différentielle qui n'admet pas de solution simple.
En revanche, si x petit devant L, tu peux faire un développement limité de Taylor de Ep=f(x) au voisinage de x= 0 et là : tu obtiens quelques chose de simple qui devrait te paraître familier... Mon message précédent devrait t'aider....

Merci beaucoup pour ton aide,tout est vraiment plus claire !

Bonjour,je reviens ici,des petites questions me tracasse,+ du sens de la compréhension pratique d'un tel dispositif.

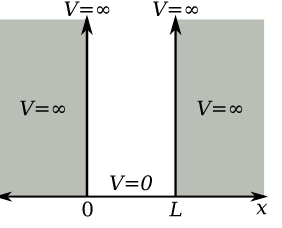
Je m'interrogeai, ce dispositif peut bien être schématisé par le schéma joint ci-dessous ?
Quel est l'intérêt pratique de ce genre de dispositif ?
De plus,nous avons vu un diagramme de phase périodique ? Quel est le sens physique que l'on peut en déduire ?

Correction,le diagramme de phase n'était pas périodique mais circulaire pardon.

Le potentiel de ton premier message correspond à un puits de potentiel de profondeur :
Ep_max Ep_min= E_o. La conservation de l'énergie mécanique, en supposant l'absence de frottement, correspond à :
Em=Ec+Ep avec Ec0; EmEp
Pour que la particule oscille dans le puits de potentiel sans en sortir, il faut  que l'énergie mécanique soit inférieure à Ep_max. Graphiquement, on voit bien que les valeurs maximale et minimale de x correspondent à l'intersection de la courbe correspondant à Ep et de l'horizontale d'ordonnée Em. Si Em>Ep_max, la particule peut sortir du puits de potentiel, il n'y a pas d'oscillations.
Le dernier schéma que tu fournis correspond à un puits de potentiel de profondeur infinie : la particule ne peut jamais sortir du puits.
Si le potentiel est de la forme Ep=½k.x², cas ici des oscillations de faible amplitude), les oscillations sont sinusoïdales. On obtient :



Si tu représentes dans un repère les variations de v(t) en fonction de x(t), tu obtiens une ellipse dont les axes de symétrie sont les axes du repère. Bien sûr, par un choix judicieux d'échelle, cela peut conduire à un cercle de centre O, l'origine du repère.

Merci beaucoup.
Donc si j'ai bien compris,sur le graphe que vous m'aviez montré avec Ep en fonction de x, on peut lire,par des segments horizontaux ,une énergie mécanique. Si cette énergie mécanique est supérieur à Ep_max alors la particule sort du puit de potentiel.
Et Ep_max correspond "à l'espèce de plateau" obtenu pour x s'éloignant de 0.

J'imagine qu'ayant une condition sur x pour que la particule oscille, on peut trouver une condition sur sa vitesse pour qu'elle oscille.

Voici une illustration graphique de mon précédent message mais je crois que tu as compris l'essentiel. Ep_max correspond pour cet exemple à soit Ep_max=E_o. La courbe bleu a pour ordonnée l'énergie mécanique Em : il y a oscillation. La courbe verte correspond aussi à une énergie mécanique Em plus élevée qui ne conduit pas à des oscillations.
L'énergie mécanique se déduit comme tu l'as écrit à partir des conditions initiales : la connaissance de l'abscisse initiale donne E_po, la connaissance de la vitesse initiale permet d'obtenir E_co et E_m=E_co+E_po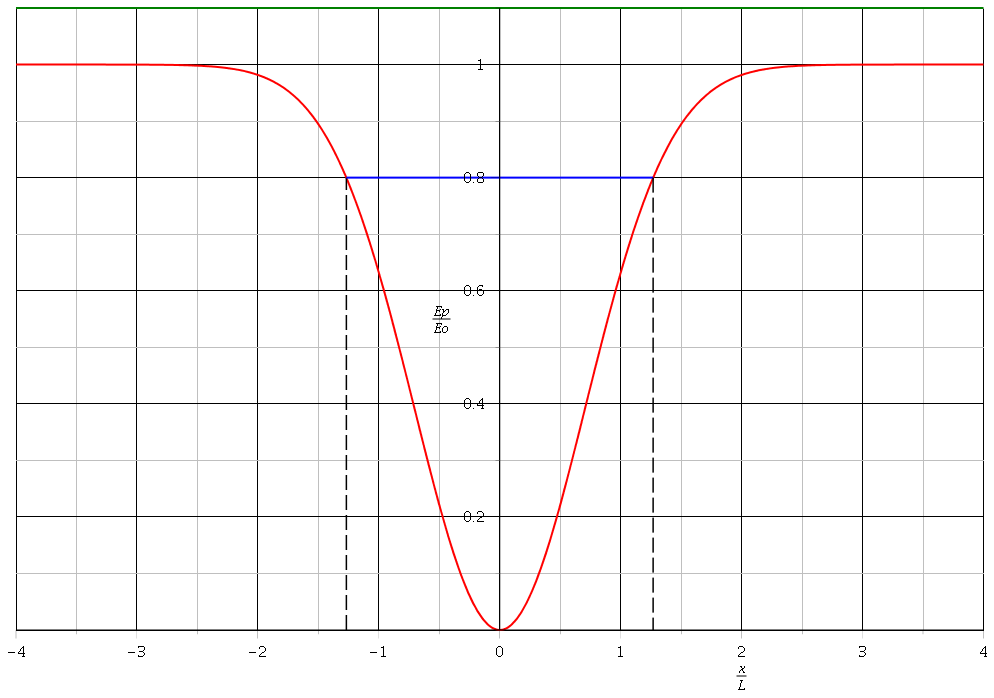

Bonsoir, merci infiniment, ces schemas confirment bien ce que j'avais compris. Dernière petite interrogation en m'excusant de vous déranger, pourquoi n'y a t-il plus/pas d'oscillation pour E_p > E_pmax?

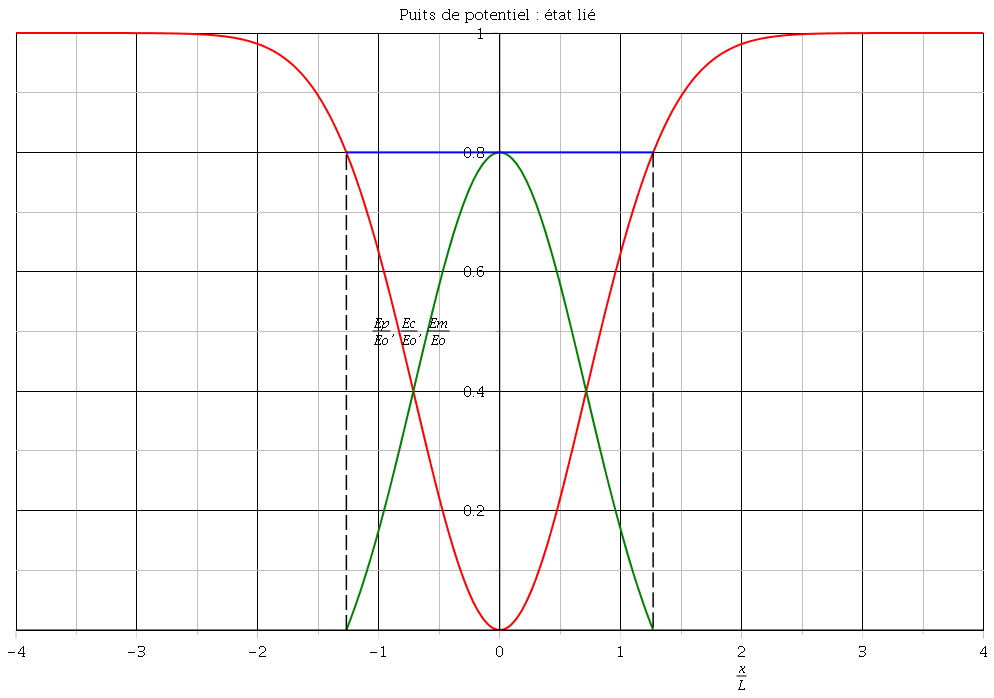
Pour une meilleure clarté, je reprends les courbes en y ajoutant, en vert, les variations d'énergie cinétique.
Premier cas : Em<Ep_max . Puisque Em=Ep+Ec avec Ec0, cet état ne peut exister que si l'horizontale correspondant à Em (en bleu) est au-dessus de la courbe correspondant à Ep (en rouge).  Lorsque ces deux courbes se coupent, la vitesse s'annule et la particule repart en sens inverse. La particule oscille sans pouvoir sortir du puits de potentiel. On parle d'état lié. Bien sûr, l'énergie cinétique est maximale quant l'énergie potentielle est minimale.
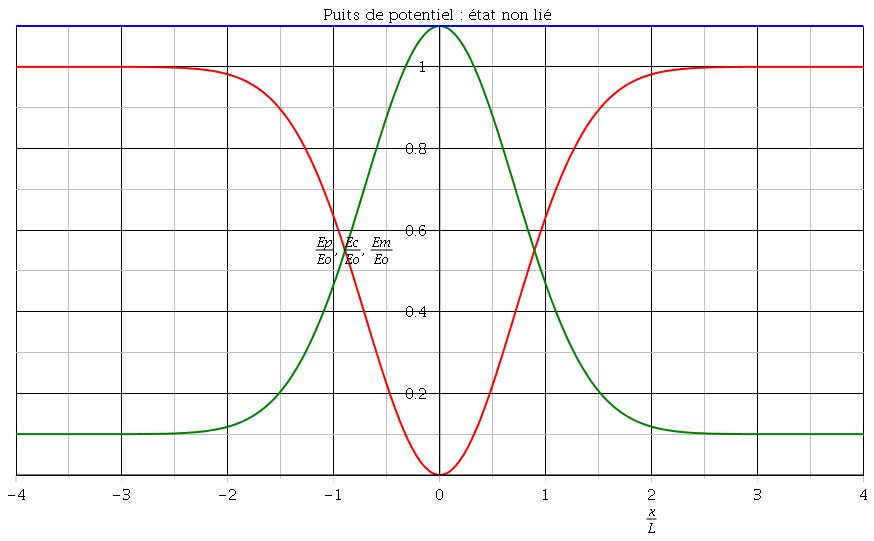
Deuxième cas : Em>Ep : Ec=Em-Ep ne s'annule jamais : la vitesse de la particule ne change jamais de sens, il n'y a plus d'oscillations. Imaginons par exemple la particule en x=-4L, avec une vitesse orientée dans le sens positif de sorte que l'énergie cinétique soit 0,1Eo et l'énergie potentielle Ep=Eo, ce qui correspond à Em=1,1Eo (voir second graphe). La vitesse de la particule va augmenter jusqu'à la position x=0 puis diminuer ensuite jusqu'à retrouver, en x= 4L sa valeur initiale.

Merci beaucoup !!

Je reviens encore,désolé
En faisant un graphe . Je ne comprends pas pourquoi avec mon "cercle" n'est pas fermé,voici le graphe :

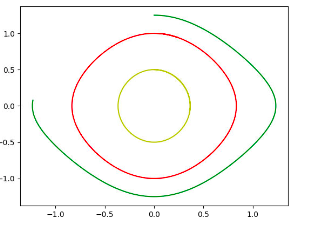
J'imagine que l'intervalle de temps sur lequel tu demandes le tracé est inférieur à une période. Pour t'en dire plus, il faudrait que tu précises le logiciel que tu utilises pour le tracé et la procédure utilisée.

Bonjour,j'ai testé sur python avec euler ou odeint. Pourquoi le temps influencerait sachant qu'il s'agit ici seulement de x ?

A mon avis, inutile de résoudre l'équation différentielle numériquement. Si tu veux le faire, il faut savoir que la période des oscillations augmente avec l'amplitude quand Em n'est pas faible devant Eo, ce qui peut justifier mon message précédent. Plus simplement :

Pour une valeur donnée de Em, la vitesse est donnée par la relation :



Il suffit de représenter les variations de v(x) en fonction de x et de -v(x) en fonction de x.

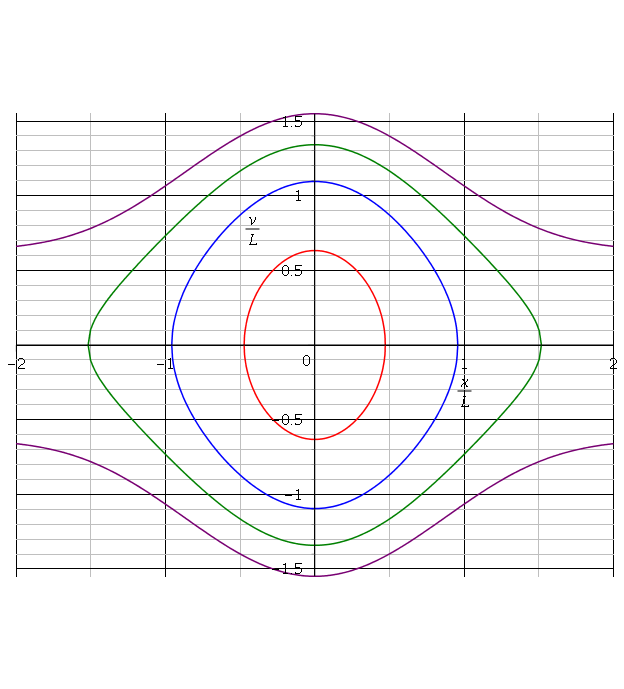
Voici le résultat que j'obtiens :

*courbe rouge : Em=0.2Eo : les oscillations sont pratiquement sinusoïdales : le diagramme des phases correspond à une ellipse dont les axes du repère sont les axes de symétrie ;

*courbe bleue : Em=0.6Eo : les oscillations ne sont plus sinusoïdales ; le diagramme n'est plus assimilable à une ellipse ;

*courbe verte : Em=0.9Eo : les oscillations ne sont pas sinusoïdales mais il y a toujours oscillations ;

*courbe violette : Em=1.2Eo : il n'y a plus oscillation. La courbe du haut correspond à une vitesse positive : la particule se déplace dans le sens des x positifs ; celle du bas corrrespond à un déplacement de la particule dans le sens des x négatifs.

Merci beaucoup !

Bonjour,je reviens ici pour une question + de culture générale.

Pour savoir,les puits de potentiel ont-ils une utilité réelle ou servent-ils seulement d'appui pour comprendre les phénomènes quantiques ?

La notion de puits de potentiel intervient de façon systématique dans l'étude des oscillations. Quelques exemples classés par difficultés croissantes :
1° : oscillations verticales d'une masse accrochée à un ressort : Ep=½k.x²
2° : oscillations d'un pendule autour d'un axe horizontal : Ep=m.g.L.[1-cos()]
3° : oscillations d'une molécule :

Bonjour,

Merci,c'est donc un outil très utile !  !

Pour revenir au schéma que je vous avaient joint,pour être sur,l'énergie potentielle au sein du puit est nul et à l'extérieur elle vaut la valeur qui est joint dans l'exercice.

Tu veux sans doute parler du puits de potentiel de profondeur infinie décrit dans ton message du  31-05-20 à 11:52. L'énergie potentielle est nulle à l'intérieur et infinie à l'extérieur ; il s'agit bien sûr d'un modèle simplificateur... Cela signifie que, quelle que soit son énergie mécanique, la particule ne peut jamais sortir du puits. Ce modèle est surtout utilisé en mécanique quantique.

Oui c'est ça,donc ici la situation est celle-ci sauf que le potentiel extérieure n'est pas infini mais vaut l'expression du sujet ?

C'est cela : si le puits de potentiel est de profondeur infinie, la particule ne peut jamais en sortir. Dans le cas du puits étudié dans les messages précédents, la particule sortait du puits pour une énergie mécanique supérieure à E_o.

Merci !