Inscription / Connexion Nouveau Sujet
oscillation forcées
bonjour j'ai besoin d'aide sur cet exercice que je ne comprend pas vraiment (merci déjà pour l'aide)
le référentiel terrestre Rg(O,ex,ey,ez) est supposé galiléen.Un point M de masse m, relié à un ressort horizontal de constante de raideur k et de longueur à vide lo, peut glisser sur l'axe (o;ex) d'un plan horizontale sa position est repérée par l'abscisse x à partir de sa position d'équilibre située à l'origine O..Le point M est soumis à
=>une force de frottement fluide Ff
=>une force excitatrice sinusoïdale F =Focos(wt)
le mouvement a lieu comme si A était fixe dans Rg et la force F appliquée directement sur M. On posera w²0=k/m et (wo/Q)=(h/m)
1)Établir l'équation du mouvement de M dont x(t) est solution. Cette équation différentielle est t-elle linéaire ?
2)On cherche la réponse en élongation de l'oscillateur en régime sinusoïdale forcé.La solution particulière est de la forme x(t)=Xmcos(wt+
)
le déphasage de l'élongation représente t-il l'avance de phase ou le retard de phase de la réponse de l'oscillateur par rapport à l'excitation?
donner l'équation vérifié par l'amplitude complexe Xm
3)les résultats qui suivent sont fonction de F0 ,m, de la pulsation w de l'excitateur, de la pulsation propre w0 et du facteur de qualité Q de l'oscillateur. Établir l'expression de l'amplitude Xm des oscillations.Pour déterminer complètement la phase de x(t),donner les expressions de tan et sin. En deduire le domaine de variation de (w). La phase est t-elle une fonction croissante ou décroissante de w?
4)Pour quelles valeurs de Q y a t-il resonnance d'elongation?determiner,dans ce cas la pulsation propre wR et l'amplitude XmR
5)tracer l'allure de la courbe Xm de w dans la situation de résonnance puis en l'absence de résonnance
6)Dans le cas de l'oscillateur peu amorti où Q>>1, montrer que l'acuité de la resonnance, définie par le rapport entre la pulsation propre de l'oscillateur et de la bande passe Δw du filtre,vérifie la relation approchée: (wo/Δw)=Q
commenter la sélectivité du filtre
Pour la première question c'est déjà fais
la deuxième question je suis bloqué à l'amplitude complexe
Bonjour
Une fois obtenue l'expression du complexe, l'amplitude est le module du complexe, la phase est l'argument du complexe.
Tu pourras trouver des informations complémentaires ici :
Si tu ne t'en sors pas, poste ici l'expression du complexe associé à x, je t'aiderai un peu plus.
Bonsoir vanoise
alors j'ai eu X(t)=Xmcos(wt +)
qui s'écrit en complexes X=Xmexp (j (wt +))
= Xmexp(jwt )*exp(j)
=Xm* exp(jwt)
c'est bon?
Cela est correct mais il faut ensuite la relation donnant X(t) déduite de l'application de la relation fondamentale de la dynamique ; je veux parler de la relation faisant intervenir les caractéristiques de l'oscillateur, la pulsation et Fo.
Le document ci-dessous devrait t'aider :
alors j'ai trouvé Xm= après avoir remplacé x(t) par son expression complexe dans l'équation du mouvement
c'est bon .
Le domaine de variation de la phase initiale peut se déduire du signe de sin() que tu viens logiquement de déterminer.
Comme en math : calcul de dérivée et tableau de variations.
Remarque : si le numérateur de l'expression est une constante, tu peux te contenter d'étudier les variations du dénominateur. A un minimum de ce dénominateur, correspond un maximum de la grandeur, une diminution du dénominateur correspond à une croissance de la grandeur étudiée...etc...
Je te croyais rendu à la question 4...
Pour le sens de variation de , tu as tout intérêt à raisonner sur le sens de variation de tan() sans perdre de vue que le sinus est négatif.
enft j'ai compris après
sinon tan() est decroissante et par consequent f est une fonction decroissante de w sur son domaine de variation
En reprenant ton résultat (correct) posté hier à 23h40 et en posant : , il est possible d'écrire l'expression de l'amplitude sous la forme :
avec:
Pour étudier l'influence de la pulsation w sur l'amplitude, il suffit en fait de calculer la dérivée f'(z) et de remplir un tableau de variation comme cela se fait en math. Si f(z) augmente en fonction de z, Xm diminue en fonction de w et inversement. Je te laisse continuer. Tu vas être amené à distinguer deux cas :
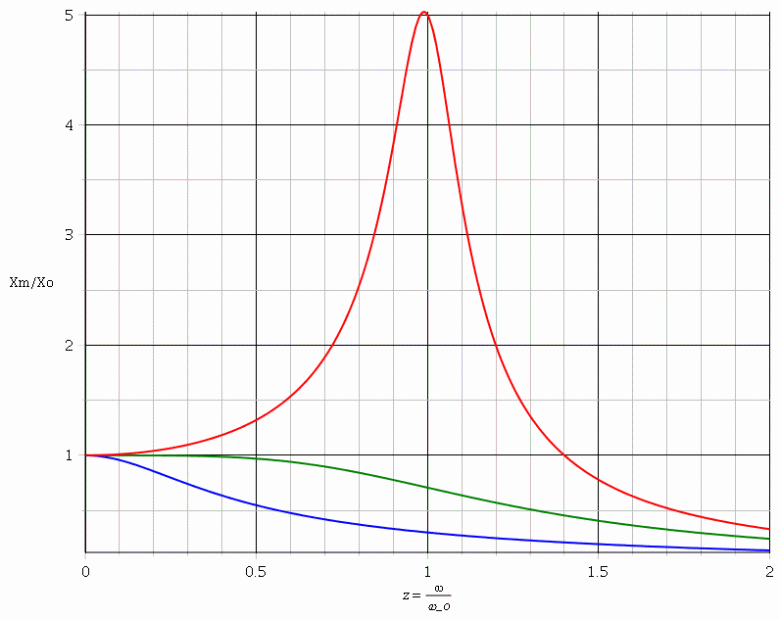
Pour t'aider un peu et t'autocorriger, voici les allures des courbes représentant les variations du rapport en fonction de
dans trois cas :
Q=5 : courbe rouge ;
: courbe verte ;
Q=0,3 courbe bleue
Les trois courbes ont deux points communs :
* z=0 correspond à Xm=Xo
*la tangente aux trois courbes en z=0 est horizontale.
On voit bien qu'un phénomène de résonance d'amplitude intervient pour ; cette résonance est d'autant plus aiguë que la valeur de Q est élevée.
Annuler
connectez vous