Bonjour ,
je fais appel à vous car je retrouve bloqué dans une de mes questions de mon dm qui m'empêche d'avancer.
mon exercice traite du mouvement d'un objet  suspendu à un ressort soumis au poids, à la force de rappel d'un ressort d'une force de frottement visqueux (Ff =
) ainsi que d'une force excitatrice Fe = Fmcos(ωt + Φl)

ce qui donne l'équation différentielle suivante:


après avoir déterminer une solution de l'équation homogène répondant aux conditions Zh(0) = 0 et Zh'(0) = vo :
Zh(t) =

après cela j'ai déterminer une solution particulière sous la forme Zmcos(ωt+Φp) (forme donnée par l'énoncé)
ce qui ma permis de trouver Zm =

et tan(Φp) =


(je précise ici que
, et


voilà maintenant la question qui me pose problème: on me demande de déduire une solution général Z(t) de l'équation différentielle lorsque  
  ainsi que lorsque Z(0) = 0 et Z'(0) = 0
cependant lorsque j'injecte Zm à ma solution particulière la somme de la solution homogène et particulière ne répondent pas aux conditions initiales, par ailleurs l'égalité
  me donne un 0 au dénominateur de tan(Φp)
Du coup je ne sais pas si j'ai fait une erreur ou si il faut revoir l'exercice et mes solutions c'est pour cela que j'aimerai avoir votre avis car cela me bloque complètement..
Merci d'avance, (edit)

Bonsoir
La solution générale est la solution particulière correspondant au régime sinusoïdal forcé
à laquelle s'ajoute la solution de l'équation homogène (régime transitoire correspondant à un second membre de l'équation différentielle nulle.
Peux-tu fournir la solution de cette équation homogène ? Il faudrait des renseignements sur les valeurs de et _o pour savoir le type de solution à retenir.
Remarque : une tangente qui tend vers l'infini ne pose pas de problème particulier, l'angle tends vers + ou -/2 selon le signe du sinus.

Le sujet ne me donne aucune information sur les valeur de , quant à la solution homogène j'avais trouvé ça mais c'était selon les conditions z(0) = 0  et z'(0) = 0 mais pour les nouvelles condition je ne sais pas si je doit trouver une solution qui répond aux conditions z(0) = 0 et ou si je doit attribuer des valeurs à ces conditions qui doivent s'annuler avec d'autres conditions initiales de la solution particulière.

ce qui me perturbe aussi c'est la formulation de la question qui commence par "en déduire" ce qui me laisse penser que je dois me servir de ce que j'ai fait avant mais quand j'essai d'appliquer ce que j'ai fais ça ne marche pas.

Mon premier message a été posté avant que n'apparaisse ton second message où les formules apparaissent en clair, ce qui facilite la compréhension...
Tu as bien étudié les deux régimes séparément : très bien. Je suis d'accord avec ton résultat correspondant au régime sinusoïdal forcé. Pour terminer, tiens compte des deux remarques :
1° celle correspondant à la dernière phrase de mon message précédent sur la phase .
2° : à propos de la solution de l'équation homogène : tu as déterminé les constantes intervenant dans la solution en considérant que cette solution vérifie : Zh(0) = 0 et Zh'(0) = vo. c'est une erreur et, je crois, la cause de tes problèmes : c'est la somme de cette solution et de la solution précédente , c'est à dire la solution générale, qui doit vérifier les conditions initiales...

je suis pas sure d'avoir compris votre seconde remarque, je dois modifier les conditions initiales pour ma solution homogène ?

En relisant l'ensemble des deux messages, je constate que tu parles de deux conditions initiales différentes :
z=0 et z'=Vo d'une part ;
z=0 et z'=0 d'autre part.
Dans mon message précédent; j'ai retenu la première, peut-être à tort. Clarifie cela ainsi que la phase initiale de la force d'excitation.
Dans tous les cas, sous réserve que les frottements restent suffisamment faibles pour que le régime transitoire soit pseudo périodique, les conditions initiales doivent être vérifiées par :


Pas toujours très facile d'aider sans un énoncé intégral... Tu n'as pas dit non plus à quelle position correspond z = 0.

La valeur de Z correspond au déplacement par rapport à la position d'équilibre, donc z = 0 correspond à la position d'équilibre du point M (excusez moi j'ai oublié de le préciser), par ailleurs les conditions Z(0) = 0 et étaient des conditions imposés  pour trouver la solution homogène dans une question précédente,
les conditions Z(t) avec Z(0) = 0 et   = 0 sont les conditions qui ont été imposé dans ma question (ces conditions sont ici appliqué à la solution générale)

Par ailleur , est ce que le Zm que vous avez écrit dans la forme de la solution générale correspond au Zm que j'avais trouvé ou à un autre Zm à déterminer à partir des conditions initiales?

Zm est bien l'expression que tu as trouvée, à simplifier bien sûr si =_o
L'expression de que tu obtiens (qui vaut /2 si =_o) représente le déphasage de la solution sinusoïdale forcée par rapport à l'excitation f. Autrement dit, dans l'expression générale de z(t), il faut poser seulement si la phase initiale de la force est nulle. Sinon, il faut poser :

du coup en simplifiant je trouve que je peux simplifier en car j'avais
Du coup je dois faire appel aux condition initiales posés par la question pour connaitre ?

Non.  La valeur de Phi  devrait être fournie par l'énoncé.  Le plus souvent cette phase initiale de la force est choisie nulle.

au niveau de l'énoncée la seule information que j'ai c'est que la force d'excitation vaut fe = donc sa phase est nulle , donc je peux poser   ?

Oui bien sûr! Il aurait été préférable de l'écrire dès le début...

Ah oui désolé j'étais persuadé de l'avoir annoncé, désolé
du coup pour résoudre

j'ai Zm = (après simplification en remplaçant
Et en appliquant les conditions initiales qui sont Z(0)= 0 et
ça me fait A = 0 et B =

L'expression générale de z(t) est :


Je ne comprends pas la ligne suivante où intervient un Zm ... Puisque la pulsation d'excitation est égale à la pulsation propre, la relation que je viens de réécrire se simplifie :



avec :

D'accord avec tes valeurs de A et B ; d'où l'expression générale de z :



soit :



Il faudrait avoir les valeurs numériques. Il est possible que l'écart relatif entre _o et _a soit très faible...

Le sujet ne me donne aucune valeur numérique concernant et .
En tout cas je tiens à vous remercier pour l'aide que vous m'avez apporter pour cette question.

Bonsoir
Je reviens sur le calcul de la phase initiale en régime linéaire. Je n'ai pas détaillée précédemment la méthode de détermination de   et en reprenant l'intégralité du calcul, je constate une erreur de signe... Toutes mes excuses pour le caractère un peu tardif de cette mise au point... En régime sinusoïdal établi, la solution complexe vérifie :




Autrement dit :



Si on pose :   et tex]z_{p}=Z_{m}\cos\left(\omega.t+\Phi_{p}\right)[/tex]





Avec   car la partie imaginaire du complexe dont on prend l'argument est négative. C'est cette remarque qui n'a pas été prise en compte dans les messages précédents. Le cas   conduit donc à . Ce qui conduit à inverser les signes dans l'expression de zp(t) puis de la solution générale qui s'écrit en définitive :



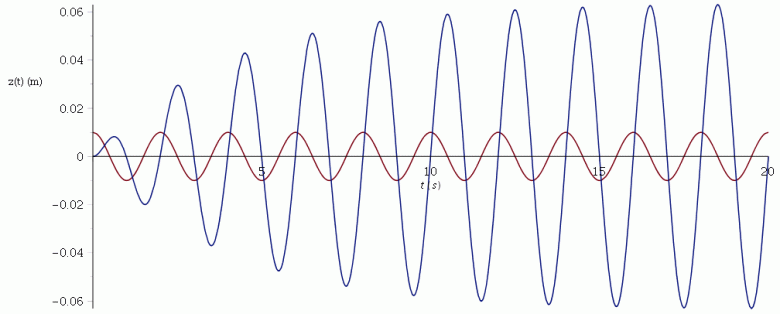
Pour visualiser le résultat, je me suis intéressé au cas numérique suivant, arbitraire mais assez réaliste :



La solution générale de cette équation est :



Voici, en bleu, la courbe représentant les variations en fonction de t de z(t) et en rouge, la courbe représentant les variation de la force f (échelle verticale arbitraire). Tu remarqueras qu'au bout d'environ 6 périodes d'excitation, la composante transitoire z_h(t) est devenue totalement négligeable, z(t) devenant pratiquement égal à z_p(t). C'est pour cette raison que, souvent, les problèmes se limitent à l'étude du régime sinusoïdal forcé. Cette remarque est aussi valide en électrocinétique : quand on relit un circuit passif à un générateur de tension sinusoïdale, on ne s'intéresse en général qu'au régime sinusoïdal forcé.