Inscription / Connexion Nouveau Sujet
Oscillateurs mécaniques en régime sinusoïdal forcé
Bonsoir , n'ayant pas bien compris le cours sur le régime sinusoïdal forcé je nécessite votre aide sur quelques questions à propos de ce sujet
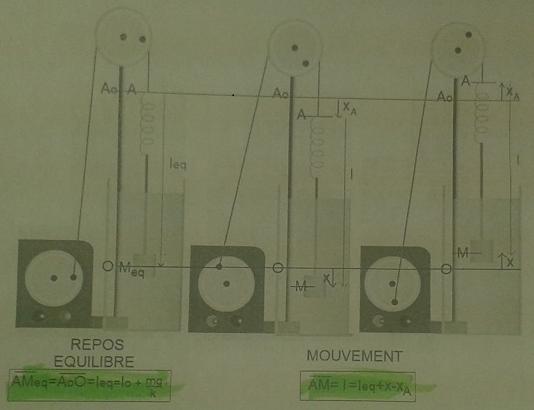
Enoncé : La masse m assimilable à un point matériel M est suspendue à un ressort(raideur k, longueur à vide l0). L'extrémité supérieure A de ce ressort serait en A0 si elle était immobile mais elle est animée d'un mouvement sinusoïdal autour de A0 d'élongation =xA(t)=a
2
cos(
t) . Le point M est soumis en plus de son poids et de la tension du ressort à une force de frottement fluide
Questions : 1) Faire le bilan des forces et chercher la longueur du ressort leq à l'équilibre quand l'extrémité A n'oscille pas. On prendra l'origine O des abscisses sur l'axe vertical( x(t) = ) tel que
=leq.
2) Appliquer le principe fondamental de la dynamique au point M en mouvement et montrer que tout se passe comme si M était soumis à trois forces que l'on identifiera.
3) Faire l'analogie avec les grandeurs électriques
4) Ecrire l'équation différentielle vérifiée par x(t) sous forme canonique en définissant la pulsation propre et le facteur de qualité. Montrer que x(t) = +
0/Q+
02 = 02Q2cos(t)
Pour ma part , j'ai trouvé pour la 1) :
en remplaçant on obtient mg - k(l0 + mg\k) -
Pour la 2) : =
mais je ne comprends pas où il faut en venir
Pour la 3) Les analogies électriques sont x=q ; v=i ; m=L ; h=R ; k=1\C mais là non plus je ne vois pas trop où il faut en venir
Merci d'avance pour votre aide
Bonsoir tris34,
c'est un problème classique mais vu l'heure je ne peux pas te répondre maintenant (il y a trop de formules à taper !). Comme je vois que tu es connecté, tu peux regarder ici (clique sur la maison) : 
.
Demain on reprendra ça en détail, si aucun correcteur ne s'est manifesté.
Bonne nuit.
?ouais ^^ mais ce chapitre jai pas bien compris ....
La on obtient mg -k(leq -l0) = 0 et apres ca avance à rien de remplacer lexpression entre parenthèses par mg/k ...
la question 1) n'a rien à voir avec les oscillateurs! c'est un bête équilibre de 2 forces
mg -k(leq -l0) = 0 donc leq = ...
ben leq vaut (mg/k) +l0 . Mais apres le fait de prendre O l'origine des abscisses sur laxe vertical on n'a pas besoin de sen servir pour la 1 ?
Pour la 2 on applique la deuxieme loi de Newton et les trois forces cest le poids , la tension et la force de frottement ?
moui mais il faut répondre à
montrer que tout se passe comme si M était soumis à trois forces que l'on identifiera
Oui apres on divise par m de chaque côté pour faire apparaitre le facteur de qualité et la pulsation non ?
Annuler
connectez vous