Inscription / Connexion Nouveau Sujet
Oscillateurs harmoniques couplés
Bonjour,
J'aurais besoin d'une explication s'il vous plait, à propos des oscillateurs harmoniques couplés non amortis.
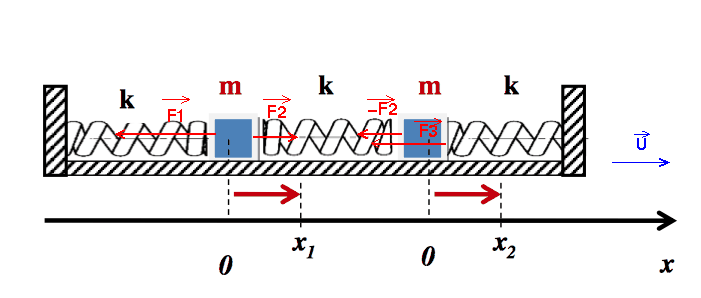
On considère deux points matériels de même masse m et reliés à trois ressorts de même longueur
, de même constante de raideur k selon le schéma ci-dessus.
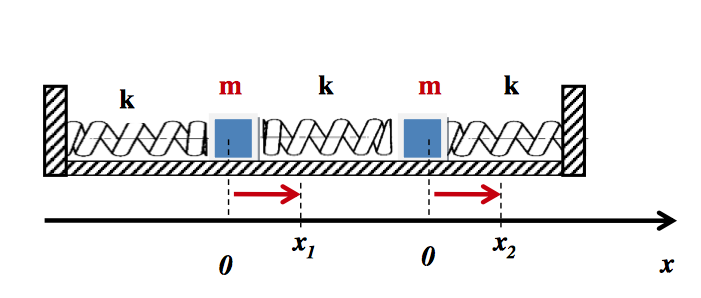
On écarte le système de sa position d'équilibre en déplaçant l'une ou les deux masses et en lâchant l'ensemble.
On appellera et
les abscisses des deux masses par rapport à leurs positions d'équilibre.
Résolutions:
Bilan des forces:
Masse 1:
Comme pas de mouvement suivant l'axe des y:
Je ne vois pas comment écrire pour les deux autres forces
On obtient d'après le PDF suivant l'axe des mouvements c'est à dire l'axe des x:
On trouve:
, or que vaut: et que vaut
.
Est-ce la force de rappel du ressort ? C'est seulement que je n'ai pas compris.
Cordialement,
CloudNine,
Bonsoir
x1 et x2 représentent les élongations des deux masses, c'est à dire leurs déplacement algébriques par rapport à la situation d'équilibre correspondant aux deux masses immobiles, les ressorts ayant leurs longueurs à vide. Le schéma me semble explicite à cet égard.
Pour la première masse, l'accélération peut s'écrire :
Ce qui va te donner une première équation différentielle.
L'étude du mouvement de la seconde masse va te fournir une autre équation différentielle.
Attention aux signes... Imagine par exemple une situation où x2>x1 : le ressort central est ainsi plus long qu'à vide. Quels sont alors les sens des forces que ce ressort exerce sur la masse de gauche et sur la masse de droite ?
Je te laisse réfléchir et proposer les deux équations différentielles...
Bonsoir vanoise,
Merci pour votre réponse,
C'est le schéma qui se trouve dans mon cours de physique.
J'ai bien compris pour x1 et x2 qui représente les élongations des deux masses, et x1-x2 est l'allongement, la différence de longueur avant et après déformation.
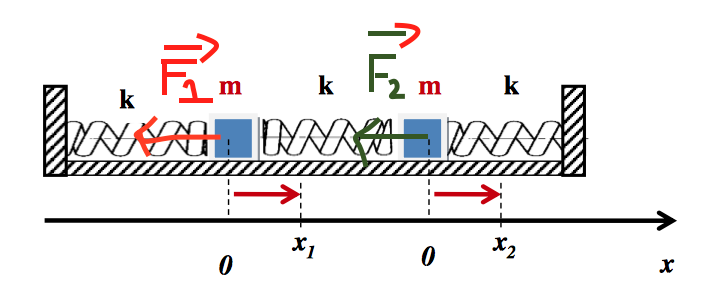
Avec
Ce que je ne comprends pas c'est que représente: " "? C'est seulement ça qui me bloque.
Sinon, on applique le PFD (selon la deuxième loi de Newton) selon l'axe des mouvements, c'est à dire l'axe des x:
Ensuite, je sais comment résoudre l'équation différentielle.
Il faut ensuite posé X1= x1+x2 et X2=x2-x1
Afin de trouver la solution générale: X1=A1sin(wot + phi1) et X2=A2sin(sqrt(3)wot+phi2)
Tu as bien fait de poster un schéma. Je comprends ainsi mieux tes difficultés.
Supposons x2>x1 sur la figure. Par rapport à sa longueur à vide (cas x1=x2=0) le ressort central est allongé de x2 et raccourci de x1 ; (x2-x1) représente donc l'allongement du ressort central. Ce ressort central tend spontanément à retrouver sa longueur à vide, il exerce donc sur la masse de gauche la force :
Il exerce sur la masse de droite la force opposée. Le ressort de droite exerce sur la masse de droite la force :
Le corrigé que tu as sous les yeux devrait te permettre de terminer. Sinon : n'hésite pas !