Inscription / Connexion Nouveau Sujet
Oscillateurs couplés
Bonjour j'ai déjà du mal pour un exercice sur un Oscillateurs Simple mais la j'ai un exercice sur un Oscillateurs couplés.
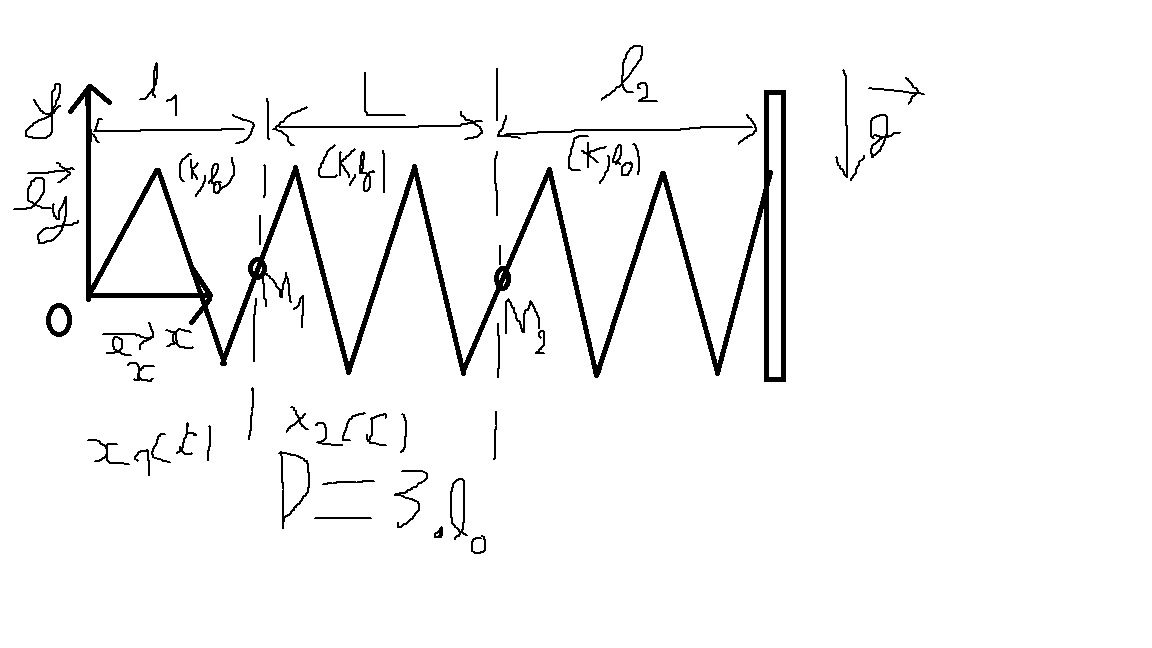
On considère un système consitué de deux oscillateurs et reliés par un ressort central .
Les extrémités 0 et E sont fixes: la distance D= 3l0 est donc constante
Les trois ressorts sont identiques : même longueur à vide l0 et même constant de raideur k. De même pour les masses des deux masselottes on a :
m1=m2=m=500g
A un instant t quelconque, On notera l1,l2 et L la longueur des ressorts
La position de la première masselotte est repérée par la position du point M1:
On notera x(t) la position du point M2: On notera x2(t) la distance entre M2 et l'origine 0.
1- En appliquant la relation fondamentale de la dynamique M1, montrer que l'équation différentielle vérifiée par x1(t) est :
(x_t (t)+w^2 (2x_1 (t)-x_2 (t))=0) ̈
Bonjour
La clé de la réussite dans ce genre d'exercice est la clarté des schémas. Commence par représenter la situation d'équilibre où les 3 ressorts ont leurs longueurs à vide. Juste en dessous represente une situation quelconque où la masse m1 est décalée vers la droite de x1 et la masse m2 décalée vers la droite de x2. Tu vas constater que le ressort de gauche est allongé de x1, que le ressort central est allongé de (x2-x1) en supposant x2>x1. Le ressort de droite est raccourci de x2. Sachant que chaque ressort exerce une force de façon à chercher à revenir à sa longueur à vide, tu devrais pouvoir représenter les vecteurs forces exercées sur chaque masse. Ensuite il faut appliquer la RFD à chaque masse.
Noter x la position d'un point comme tu l'écris n'a pas de sens. Au moins dans un premier temps, tu as tout intérêt à adopter mes notations. x1 désigne l'élongation de M1 c'est à dire son déplacement algébrique par rapport à sa position d'équilibre. x2 désigne l'élongation de M2 c'est à dire son déplacement algébrique par rapport à sa position d'équilibre. Il faut je pense imaginer cet oscillateur pouvant glisser sans frottement sur un plan horizontal de sorte que les poids soient compensés par les réactions du plan et n'interviennent donc pas dans cette étude. Ton schéma est vraiment peu clair et ne t'aide pas vraiment...
Commence par essayer de comprendre ce que je t'ai expliqué en faisant un schéma soigné et suffisamment grand. Je te conseille de le faire dans le cas x1>0 et x2>x1. Essaie alors d'y représenter les différents vecteurs force. Cela t'aidera pour l'application de la RFD à M1 puis à M2. Le corrigé figure sur le document que je t'ai indiqué à un petit détail près. Il faut poser ko=k car dans ton problème les 3 ressorts sont identiques. Essaie de travailler tout cela personnellement. Tu postes tout de même au niveau math sup... Tu peux néanmoins poster à nouveau sur des points précis que tu ne comprends pas.
En reprenant les notations correspondant au document fourni, on peut remarquer, dans le cas x1>0 et x2>x1 :
Le ressort de gauche est allongé de x1 par rapport à sa longueur à vide ; il exerce sur M1 une force vers la gauche d'intensité k.x1.
Le ressort central est allongé de (x2-x1) : i l exerce sur M1 une force vers la droite d'intensité k(x2-x1). La RFD, appliquée à M1, en projection sur l'axe horizontal orienté vers la droite peut s'écrire :
Je te laisse simplifier... Tout cela est sur le document que je t'ai indiqué.
Ok merci beaucoup j'ai réussi à faire la simplification mais pour l1 masse M2 on à la même dans dire avec = 3 02l0
02l0
Toujours avec les même conventions :
Le ressort central exerce sur M2 une force opposée à celle exerc.e sur M1 ;
Le ressort de droite est comprimé de x2. Il exerce donc sur M2 une force vers la droite d'intensité k.x2. D'où l'équation différentielle :
Tu n'as pas bien compris la signification des élongation x1 et x2. Pour obtenir deux accélérations nulles à chaque instant, il faut :
x1=x2=0 à chaque instant.
Chaque ressort a sa longueur à vide lo.
Reprends les deux équations différentielles et considèrent les deux accélérations nulles à chaque instant. Cela te conduit au système d'équations suivant :
x1=2x2
2x1=x2
Revois ton cours de math : ce système admet comme solutions uniquement :
x1=x2=0  t.
t.
Relis mon message de 19h21 et regarde le schéma fourni sur le document que je t'ai indiqué.
Comme déjà dit, les définitions que tu as fournies de x1 et x2 sont incohérentes. J'ai donc choisi celles du document que je t'ai fourni qui sont les plus fréquemment utilisées dans ce type de problème. S'il y a une adaptation à faire, cela ne devrait pas poser de difficulté au niveau math sup !
Pour la suite de l'exercice voici la dernière question
Dans les conditions de l'expérience, la résolution des équations précédentes conduit aux solutions représentées sur la figure 3. On constate que ces solutions son sinusoïdales :Les mouvements de M1 et M2 sont donc sinusoïdaux
Ensuite j'ai un schéma avec les deux périodes x(t) en fonction du temps
Et voila les questions :
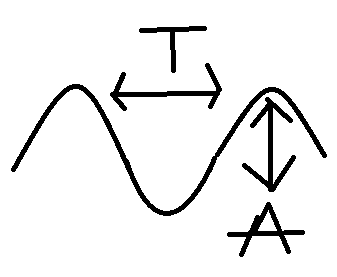
Mesurer la périodes des Oscillations
Pour cela j'ai prit le temps entre 2 points culminant de l'oscillation et j'obtient 0,6 s
(Les deux oscillations sont déphasé donc x_1+x_2=0
Ensuite je dois mesurer les amplitudes j'ai donc calculer l'amplitude entre un minima et un maxima
Ensuit on nous demande le déphasage entre les 2 oscillation donc 0
Mais la je bloque on me demande un schéma a différent moments:
t=0
t=T/4
t=3T/4
Salut,
Comme tu as explicitement demandé mon aide pour ce post (dans un autre topic) et que les autres aideurs ont l'air d'être absents depuis un bon moment, je t'aide un peu (à toi de compléter les vides que je laisse)
Si tu as choisi ce qui semble demandé dans l'énoncé (pas des plus clairs), soit x1 l'abscisse de la masse m1 et x2 l'abscisse de la masse m2 (avec O pour origine de l'axe des abscisses de direction, celle des ressorts et de sens gauche vers droite.)
On arrive au système :
d²x1/dt² + k/m .(2x1 - x2) = 0 (1)
d²x2/dt² + k/m .(2x2-x1 - 3Lo) = 0
(Si tu as choisi x1 et x2 comme les élongations, contrairement à ce que l'énoncé préconise, mais comme c'est souvent fait ... c'est presque pareil, sauf que le Lo disparait des équations différentielle du système).
En éliminant x2 dans le système ci-dessus :
(1) --> x2 = 2x1 + m/k * d²x1/dt² et en remettant cela dans (2), on arrive à :
Les solutions de l'équation caractéristique : m²/k² * r^4 + 4.m/k r² + 3 = 0 sont faciles à trouver (équation bicarrée).
Tu devrais trouver 4 solutions : ,
;
et
On a donc
On peut trouver x2(t) en utilisant l'expression de x1(t) ci-dessus dans x2 = 2x1 + m/k * d²x1/dt²
Il faut déterminer les valeurs des constantes C1, C2, C3 et C4 par les conditions initiales.
Suivant ces conditions initiales, il y aura plusieurs modes de fonctionnement possibles.
Soit 2 oscillations combinées de pulsations et
, soit une seule de ces pulsations.
Sauf distraction.