Inscription / Connexion Nouveau Sujet
Oscillateur sur un plan incliné
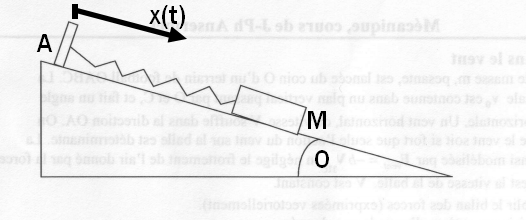
Soit un point matériel M, de masse m, contraint à se déplacer sur un plan incliné d'un angle  . Ce point est relié par un ressort de raideur k et de longueur au repos l0 à un point A fixe situé en haut du plan incliné. Le mouvement de M est ralenti par des frottements fluides dont la force vaut -h
. Ce point est relié par un ressort de raideur k et de longueur au repos l0 à un point A fixe situé en haut du plan incliné. Le mouvement de M est ralenti par des frottements fluides dont la force vaut -h , où h est un coefficient positif et
, où h est un coefficient positif et  la vitesse du point M.
la vitesse du point M.
La position de M est repérée par l'abscisse x descendante le long de la pente, choisie nulle en A.
1) Déterminer l'équation différentielle régissant l'évolution de x(t)
2) En déduire la valeur de la position d'équilibre xéqu
3) On appelle y la quantité (x-xéqu). Ecrire l'équation différentielle que vérifie y(t)
L'angle  varie maintenant au cours du temps, autour d'une valeur non nulle
varie maintenant au cours du temps, autour d'une valeur non nulle  0. On note
0. On note  (t) =
(t) =  0 +
0 +  (t).
(t).
Contrairement à  0,
0,  (t) peut être cnsidéré comme un angle faible.
(t) peut être cnsidéré comme un angle faible.
4) Montrer que l'équation différentielle que vérifie y(t) s'écrit désormais my''(t)+hy'(t)+ky(t)=mgcos( 0)
0) (t)
(t)
5) On a  (t) =
(t) =  m cos(
m cos( t). Déterminer y(t) en régime permanent
t). Déterminer y(t) en régime permanent
On souhaite comparer le comportement de cet oscillateur à celui d'un circuit (R,L,C) série branché à un générateur délivrant une tension sinusoïdale e(t)=Ecos( t)
t)
6) Etablir l'équation différentielle qui régit l'évolution de la charge q du condensateur dans un tel circuit
7) Si l'on réalise une analogie entre les deux systèmes dans laquelle y correspond à q, quels sont les équivalents mécaniques de R, L et C ?
8) A quelles grandeurs mécaniques correspondent les tensions et les courants ? (Justifier)
9) Quel est le lien entre E et  m
m
Pour la question 1)
On se trouve dans un référentiel terrestre, supposé galiléen.
Bilan des forces : frottement=-h x, poids=mg=mgsin
x, poids=mg=mgsin x-mgcos
x-mgcos y, support=Ry
y, support=Ry
Principe fondamental de la dynamique :  F=ma
F=ma
ma=mx''=-h +mgsin
+mgsin
Est-ce bon jusque là ? Je vous remercie d'avance
je précise: non dans ce cas précis
car une équa. diff. avec uniquement des dérivées c'est tout à fait possible
non, c'est pas la raideur non plus, mais la force de rappel du ressort
il faut être précis en physique sinon on ne se comprend plus
D'accord donc avec la force de rappel on a mx"+hx'+kx=mgsin +kl0
+kl0
Et pour la question 2) pour avoir la position à l'équilibre, c'est quand la vitesse est nulle, donc
kxéqu=mgsin +kl0
+kl0
xéqu=(mgsin )/k+l0
)/k+l0
continue jusqu'à ce que tu bloques, inutile de détailler toutes les étapes, indique juste tes réponses intermédiaires
Question 3) Je ne sais pas si c'est comme ça qu'il faut faire
y(t)=x(t)-xéqu donc x(t)=y(t)+xéqu et on remplace x(t) par sa nouvelle valeur dans l'équation (x'(t)=y'(t) comme xéqu est une constante qui ne dépend pas du temps et x''(t)=y''(t))
my''+hy'+ky=mgsin +kl0-kxéqu
+kl0-kxéqu
ce qui donne au final : my''+hy'+ky=0
Question 4) Je ne comprends pas comment le second membre qui correspond aux variations de l'angle est apparu
Q3) oui, c'est le but de la manœuvre: on élimine la constante au second membre en changeant de variable
Q4) il faut partir de: my"+hy'+ky = mgsinO -kxeq
(car le second membre dépend de t maintenant)
et utiliser le fait que alpha(t) est petit devant theta0 pour simplifier ce second membre
sachant que sin(p) - sin(q) se trouve dans tout bon formulaire de trigo, cf ![]()
Si alpha est faible son cosinus tend vers 1 et son sinus vers 0 donc au final on cos( (t))=sin
(t))=sin 0
0
Je n'ai pas compris comment on peut avoir mgcos 0
0 (t) à partir de mgsinO -kxeq et du fait que alpha soit faible
(t) à partir de mgsinO -kxeq et du fait que alpha soit faible
tu fais le changement de variable: y = x - xeq
avec xeq = mg sinOo/k - lo (position d'équilibre quand O=Oo)
ce qui donne: my"+hy'+ky = mgsinO - mg sinOo
et là, tu devrais y arriver
Merci beaucoup
my"+hy'+ky = mgsinO - mg sinOo
mg(sinO-mgsinOo)=mg(2sin((O-Oo)/2)cos((O+Oo)/2))=2mgsin( /2)cos(Oo+(
/2)cos(Oo+( /2))
/2))
Comme  est faible sin(
est faible sin( /2)
/2)
 /2
/2
2mgsin( /2)cos(Oo+(
/2)cos(Oo+( /2))
/2)) 2mg(
2mg( /2)cos(Oo)
/2)cos(Oo)
 mgcos(Oo)
mgcos(Oo)
Question 5) my"+hy'+ky=(mg mcos(Oo))cos(wt)
mcos(Oo))cos(wt)
 y"+(h/m)y'+(k/m)y=g
y"+(h/m)y'+(k/m)y=g mcos(Oo)cos(wt)
mcos(Oo)cos(wt)
avec w0= (k/m) et Q=(m/h)
(k/m) et Q=(m/h) (k/m)=(
(k/m)=( (km))/h
(km))/h
Je ne comprends pas la question, quand ils demandent y(t) en régime permanent, ils veulent qu'on résolve l'équation c'est ça ?
Je ne suis pas très à l'aise avec les équivalents complexes, est-ce que c'est possible de plutôt faire :
Xsp = Acoswt + Bsinwt
puis Xsp' = Bwcoswt-Awsinwt
Xsp"=-Bw²sinwt-Aw²coswt
Puis on remplace les y de l'équation par la solution particulière Xsp et on résout le système (avec le second membre egal à 0 et le second membre égal à une constante) ?
Finalement j'ai utilisé les complexes comme sur la fiche que vous m'avez donné même si c'était laborieux, ça m'a permis de revoir la méthode
J'ai terminé l'exercice, encore merci pour votre aide c'était très gentil !
1)
mg.sin(theta) - k.(x - Lo) - h.dx/dt = m.d²x/dt²
d²x/dt² + (h/m).dx/dt + (k/m).(x - Lo) = g.sin(theta)
-----
2)
Si vitesse et accélération nulle ---> position de repos :
d²x/dt² + (h/m).dx/dt + (k/m).(x - Lo) = g.sin(theta)
0 + (h/m).* 0 + (k/m).(x - Lo) = g.sin(theta)
(k/m).(x - Lo) = g.sin(theta)
x = Lo + (mg/k).sin(theta)
xéqu = Lo + (mg/k).sin(theta)
-----
3)
d²x/dt² + (h/m).dx/dt + (k/m).(x - Lo) = g.sin(theta)
x = y + xequ
d²(y + Lo + (mg/k).sin(theta))/dt² + (h/m).d(y + Lo + (mg/k).sin(theta))/dt + (k/m).(y + Lo + (mg/k).sin(theta) - Lo) = g.sin(theta)
d²y/dt² + (h/m).dy/dt + (k/m).(y + (mg/k).sin(theta)) = g.sin(theta)
d²y/dt² + (h/m).dy/dt + (k/m).y = 0
-----
4)
On repart de d²y/dt² + (h/m).dy/dt + (k/m).(y + (mg/k).sin(theta)) = g.sin(theta)
d²y/dt² + (h/m).dy/dt + (k/m).(y + (mg/k).sin(theta0 + alpha)) = g.sin(theta0 + alpha)
Avec sin(theta0 + alpha) = sin(theta0) * cos(alpha) + cos(theta0) * sin(alpha)
Avec alpha petit, on a l'approximation : cos(alpha) = 1 et sin(alpha) = alpha
On a donc l'apprproximation : sin(theta0 + alpha) = sin(theta0) + cos(theta0) * alpha
d²y/dt² + (h/m).dy/dt + (k/m).(y + (mg/k).(sin(theta0) + cos(theta0) * alpha)) = g.(sin(theta0) + cos(theta0) * alpha)
d²y/dt² + (h/m).dy/dt + (k/m).(y + (mg/k).cos(theta0) * alpha) = g.cos(theta0) * alpha(t)
Comme alpha est petit, on a (mg/k).cos(theta0) * alpha negligeable devant y et donc :
d²y/dt² + (h/m).dy/dt + (k/m).y = g.cos(theta0) * alpha(t)
-----
5)
Avec alpha(t) = alphaM.cos(wt) --->
d²y/dt² + (h/m).dy/dt + (k/m).y = g.cos(theta0) * alphaM.cos(wt)
Equation à résoudre ...
Mais comme on veut le régime permament (et que le mouvement est sinusoïdal), on peut remplacer d()/dt par jw et d()²/dt² par j²w²
j²w²y + (h/m).jwy + (k/m)y = g.cos(theta0) * alphaM.cos(wt)
j²m.w²y + h.jwy + k.y = mg.cos(theta0) * alphaM.cos(wt)
y(k - mw² + jhw) = mg.cos(theta0) * alphaM.cos(wt)
y = mg.cos(theta0) * alphaM.cos(wt)/(k - mw² + jhw)
y = (mg.cos(theta0) * alphaM.cos(wt))*((k - mw² - jhw))/((k - mw²)² + h²w²)
y = (mg.cos(theta0) * alphaM.cos(wt))*(k - mw²) + h.(mg.cos(theta0) * alphaM * w.sin(wt)))/((k - mw²)² + h²w²)
Après avoir vérifié (et corrigé si erreur bien possible) on développe ... ou non, on a bien une forme de y = f(t)
-----