Inscription / Connexion Nouveau Sujet
Oscillateur libre.
Bonjour,
Merci d'avance. 
Au cours des travaux pratiques dans le laboratoire d'un lycée scientifique sur les oscillations d'un pendule élastique horizontale sur un banc à coussin d'air, les élèves d'une classe de terminale ont tracé à partir des domées enregistrées.
La caractéristique ci-dessous représentée.
Le pendule élastique utilisé est de masse m et de raideur k.
On engage ce système sur un axe horizontal . Les frottements sur l'axe sont négligés.
Le professeur de physique chimie ayant en charge cette classe récupère la caractéristique et demande à chaque élève de déterminer la vitesse de l'extrémité du ressort lorsque son élongation est de + 1 cm.
Elant élève de cette classe,
1. Nomme la caractéristique représentée par ce groupe d'élèves.
2. Montre que le système effectue des oscillations libres.
3. Déduis l'amplitude xm du mouvement de ce pendule.
4. Determine la raideur k du ressort utilisé.
5. Donne la valeur de l'énergie cinétique lorsque le centre d'inertie du solide soudé à l'extrémité du ressort
occupe les positions d'abscisses et
.
6. La période des oscillations est égale à 0,628 s. Détermine la vitesse de l'extrémité du ressort lorsque l'élongation
est égale à + 1 cm.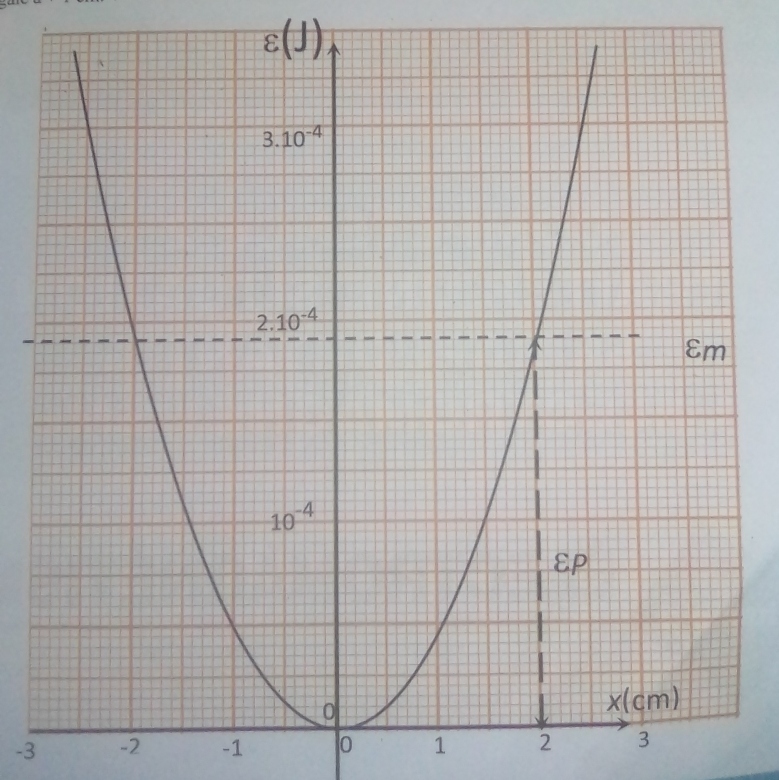
Réponses
1) La caractéristique représentée est l'amplitude maximale Xm de l'oxillateur.
2) La caractéristique représentée est celle d'une fonction sinusoïdale.
Donc le système effectue des oscillations libres.
3) Assez abstrait sur le schéma..
Bonjour
De quelle caractéristique parles-tu exactement ? De la courbe joint à ton premier message ? Rappelle-toi l'expression de l'énergie potentielle élastique du ressort.
Oui
Comment est-ce que je peux savoir si c'est l'énergie potentielle élastique ou de pésanteur ou l'énergie cinétique ou l'énergie mécanique ?
Lis bien ma réponse sur l'autre sujet concernant l'énergie potentielle élastique. Si tu l'appliques à cet oscillateur : tu constates qu'ici, l'allongement du ressort à l'équilibre est nul. L'énergie potentielle élastique du ressort s'écrit donc :
Je te laisse réfléchir et identifier la courbe fournie.
C'est bien cela. A été ajouté dans le même repère la courbe Em=f(x). Il s'agit évidemment d'une horizontale car l'énergie mécanique reste constante en absence de frottement.
Attention : cette énergie mécanique n'est en fait définie que sur un intervalle précis de x...
Sur quel intervalle ?
2) L'énergie mécanique reste constante.
Donc l'énergie mécanique du système de conserve.
Or l'énergie mécanique d'un oxillateur non amorti se conserve.
Le système effectue donc des oscillations libres.
Ok pour la conservation de l'énergie mécanique mais le "donc " à la fin est en trop. L'énergie mécanique se conserve en absence de frottement pour tout système mécanique, pas seulement pour les oscillateurs.
Sachant que :
Em=Ec+Ep avec Ec
0 , quelle inégalité entre Em et Ec cela implique-t-il ? Celà devrait te permettre de répondre à mon message précédent et à la question sur les oscillateurs.
cette énergie mécanique n'est en fait définie que sur un intervalle précis de x...
Sur quel intervalle ?
L'énergie mécanique reste constante.
Donc l'énergie mécanique du système de conserve.
Oui.
Or l'énergie mécanique d'un oxillateur non amorti se conserve.
Le système effectue donc des oscillations libres.
Le "donc" n'est pas rigoureux comme expliqué hier dans mon message du 06-03-21 à 22:31.
Je me répète :
sachant que :
Em=Ec+Ep avec Ec
0 , quelle inégalité entre Em et Ep cela implique-t-il ? Cela devrait te permettre de répondre aux questions 2 et 3.Em = Ec +Ep avec Ec ≥ 0
Si Ec =0 , Em =Ep (1)
Si Ec >0 , Em > Ep (2)
D'après (1) et (2) , Em ≥ Ep
Mais je ne comprends pas pourquoi Ec ≥ 0..
Mais je ne comprends pas pourquoi Ec ≥ 0..
Ec=½m.v2
Que peux-t-on dire du carré d'un nombre réel, positif, négatif ou nul ?
Em-Ep=Ec=½m.v2
Em-Ep0
donc :
EmEp
Reprends maintenant les courbes : seules les valeurs de x telles que EmEp sont possibles donc : sur quel intervalle de valeurs peut varier x ?
Si tu comprends bien cela, tu as les réponses aux questions 2 et 3.
Il suffit de bien regarder le graphique : le domaine d'existence physique de x est le domaine tel que la parabole Ep=f(x) est au-dessus de l'horizontale d'ordonnée Em.
Cela conduit à :
-2cm
x2cm
Or, pour un mouvement d'oscillation, l'amplitude Xm est, par définition, la valeur maximale que peut atteindre x. Par identification : Xm=2cm.
l'abscisse x varie entre deux positions symétrique par rapport à la position d'équilibre -Xm et +Xm : il y a bien oscillations.
Une fois le pendule écarté de sa position d'équilibre, on le laisse osciller librement, sans exercée sur lui de force supplémentaire, on parle d'oscillations libres.
Pour trouver la valeur de k, on peut partir de la formule générale de l'énergie potentielle élastique d'un ressort et l'appliquer, par exemple, au point d'abscisse x= Xm.
Pour utiliser le système d'unités internationales, il faut exprimer l'allongement du ressort en mètre.
Ah oui.
4)
Donc
Lorsque le ressort est à son amplitude maximale Xm=2.10-2 m , son énergie potentielle
Donc
Annuler
connectez vous