Bonjour,
Je fais un DS trouvé sur Internet (guise d'entraînement), et en fait je suis bloqué au bout de quelques questions, et je voudrais savoir si quelqu'un pourrait me débloquer.. .


Voici le sujet :

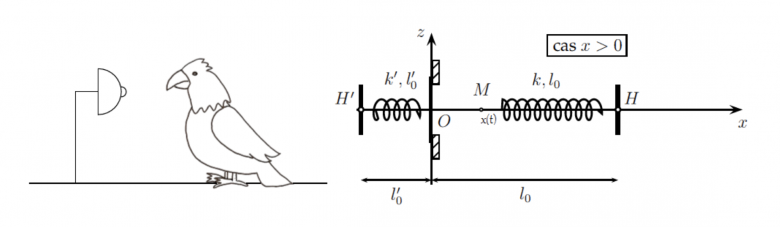
On étudie le mouvement d'un jouet appelé oiseau carillonneur. Le jouet est représenté ci-dessous à gauche et est constitué d'un oiseau qui peut se déplacer horizontalement et venir frapper une sonnette.
Afin de simplifier le problème, on se propose d'adopter la modélisation représentée ci-dessous à droite : l'oiseau sera remplacé par un point matériel M de masse m, repéré par son abscisse x. Ce point est attaché à un ressort de raideur k et de longueur à vide l0 . Le point d'attache de ce ressort est le point H d'abscisse l0 pour simplifier les calculs.
Pour modéliser le choc du nez de l'oiseau contre la sonnette, on introduit un deuxième ressort (beaucoup plus raide que le premier) de raideur k′ et de longueur à vide l0′ . Ce deuxième ressort se termine par une plaque verticale contre laquelle viendra taper la masse. Cette plaque est bloquée en x = 0 par deux murs et l'abscisse de la plaque est donc nécessairement négative. Le deuxième ressort est fixé en H′ d'abscisse −l0′ .
On suppose que le support horizontal sur lequel l'oiseau glisse selon Ox est bien lubrifié de façon à pouvoir négliger les frottements.

Il y a une première partie dans laquelle on enlève la partie sonnette et on a donc juste une masse M accrochée au premier ressort, et du coup j'ai fait toutes les questions.
J'ai trouvé x(t) = 0,1cos(21t) pour son équation de mouvement.

Et voilà que maintenant on rajoute la deuxième partie, pour avoir tout le système. (Je vais essayer de joindre l'image dans quelques minutes).

Et en fait j'ai les questions suivantes :
5. Exprimer les forces de rappel exercées par le ressort de droite Fd et le ressort de gauche Fg.
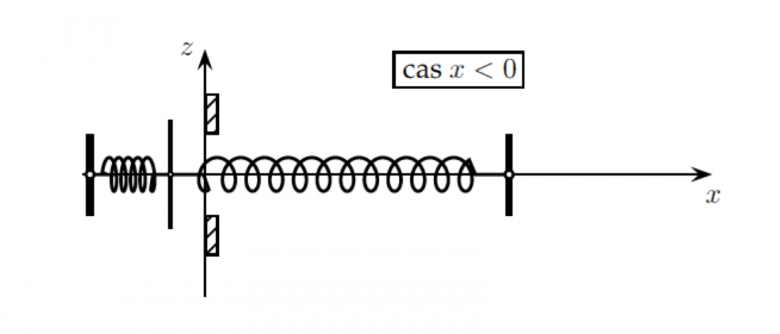
6. Quelle est la nouvelle équation différentielle régissant le mouvement du point M lorsque
x<0?
7. En déduire la nouvelle pulsation propre ω0′ et la nouvelle période T0′. Comparer T0 et T0′.
8. Les conditions initiales sont ici x(t1) = 0 et x ̇(t1) = v1. Résoudre l'équation différen- tielle compte tenu de ces conditions initiales. Attention, les conditions initiales s'ap- pliquent ici en t = t1.
9. A partir de quel instant t2 cette solution n'est-elle plus valide ?
10. A l'aide de la conservation de l'énergie mécanique, exprimer x ̇(t2) en fonction de v1.
12. Une fois que x redevient positif, quelle est l'équation du mouvement ?
13. Compte tenu de la conservation de l'énergie mécanique, quelle sera la plus grande valeur
de x atteinte ?
14. Tracer alors l'allure du mouvement complet sur deux périodes complètes.
15. Quelle est la période du mouvement en fonction de T0 et T0′ ?
16. Ce système est-il un oscillateur harmonique ? Pourquoi ?

J'ai déterminé la question 5 en trouvant comme forces pour Fg : -k'(l - l0') et pour Fd : k(l - l0).
Ensuite j'ai trouvé la nouvelle équation différentielle avec la seconde loi de Newton :
x''(t) + (k' - k / m)x(t) = 0.

Et là à la question 7 je suis bloqué, car j'ai bien la formule pour la pulsation propre mais je n'ai aucune valeur, je ne sais donc pas comment la calculer (et ensuite je suis coincé pour le reste des questions..).
Si vous avez envie de voir le sujet intégralement c'est un sujet de la prépa de Carnot à Dijon.. .
Merci beaucoup.