Salut,

Es-tu sûr d'avoir bien recopié l'énoncé ?

En effet, c'est assez délicat de te répondre si tu ne définis pas les notations dans la formule.

D'autre part cette formule de l'énergie potentielle élastique m'interpelle : Systèmes oscillants ou

En situation d'oscillations libres, sans frottement, l'équation différentielle régissant le système conduit à une solution de la forme (sans connaître les conditions initiales)

Tu sais que l'énergie potentielle élastique est de la forme :

Enfin, par définition de l'énergie cinétique :

avec

Tout d'abord je tiens a m'excuser pour ne pas avoir salue la fois passee .
Bonjour , voici l'enonce integralement
Exercice:
Un pendule élastique horizontal est constitué d'un ressort (R) de raideur *=50 N.m et de masse négligeable, enfilé à travers une
tige, à I'extrémité duquel est soudé un solide ponctuel (S) de masse m pouvant
coulisser sans frottement à travers la tige.
A I'origine des dates on écarte le solide (S) de Xo à partir de sa position
d'équilibre dans le sens positif puis on I'abandonne avec une vitesse de valeur Vo
dans le sens positif,, A un instant t quelconque, au cours des oscillations, l'élongation du solide est x et sa vitesse est y.
l. Donner I'expression de l'énergie mécanique du pendule en fonction de k, m, x et v,
2. Sachant qæ le sysême {(S), (R)} est conservatif, déduire l'équation diflérentielle régissant les oscillations du solide (S).
3. Exprimer la pulsation propre Wo en fonction de k et m et vérifier que x=xmSin(Wot+phi) et une solution générale de
l'équation différentielle obtenue.
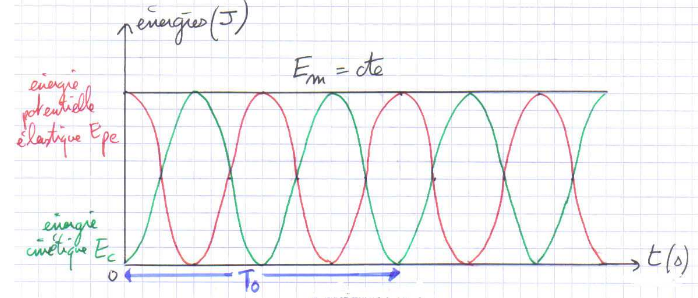
Le graphe de la figurc -l ci- dessous représente les variations de l'énergie potentielle élastique Ep du pendule au cours du
t€mps.
4.1. Établir l'expression

4.2. Déduire l'expression de l'énergie mécanique en fonction de k , x_m.
5 . Déterminer par exploitation du graphique et de ce qui précède :
5.1. La valeur de l'amplitude  Xm des oscillations, l'élongation initiate Xo du solide et la phase phi .
5.2. I-a période propre To des oscillations, la masse m du solide (S) et sa vitesse Vo initiale Vo.
Déterminer graphiquement les positions pour lesquelles, la vitesse du solide (S) est réduite à moitié de sa valeur acquise au
passage par sa position d'équilibre ?

Voici la coube

Voici la figure

Salut,

Alors si x=Xm*sin(wo.t + phi)

alors

Ep = 1/2*k*x²
Ep = 1/2*k*Xm²*sin²(wo.t + phi)

or on sait que sin²(wo.t + phi) = [1 - cos(2*(wo.t + phi))]/2

d'où Ep = 1/2*k*Xm²*[1 - cos(2*(wo.t + phi))]/2

Ep = Ep = 1/4*k*Xm²*[1 - cos(2*(wo.t + phi))]

Concernant l'énergie cinétique :

Ec = 1/2*m*v²

avec v(t) = dx/dt = ...

donc Ec = ...

puis Em = Ep + Ec = ...

Bonjour gbm, j'ai etabli la question 4.1 cependant pour la 4.2 j'ai ceci :
Ec= et Ep= en Sommant Ep et Ec j'ai finalement E=
la 5.1 c'est la premiere fois que je vois une courbe d'oscillation avec Ec en ordonnee du coup moi qui voulais determiner l'amplitude je suis a l'ouest mais pour la periode j'hesite de prendre celle de la courbe
Avant cela je veux bien qu'on me corrige la 1ere et 2eme  question car en derivant Em mes xo et vo sautent car etant des constantes donc je me retrouve avec

Si x=Xm*sin(wo.t + phi)

alors dx/dt = wo.Xm.cos(wo.t + phi)

soit Ec = 1/2*m*wo²*Xm²*cos²(wo.t + phi)

Rappel : si x(t) = sin(a.t+b) alors dx/dt = a.cos(a.t + b)

soit

Em = Ec + Ep
Em = 1/2*m*wo²*Xm²*cos²(wo.t + phi) + 1/2*k*Xm²*sin²(wo.t + phi)
Em = 1/2*m*k/m*Xm²*cos²(wo.t + phi) + 1/2*k*Xm²*sin²(wo.t + phi)
Em = 1/2*k*Xm²*cos²(wo.t + phi) + 1/2*k*Xm²*sin²(wo.t + phi)
Em = 1/2*k*Xm²

Ce qui n'est pas étonnant qu'on arrive sur une valeur constante.

En effet, tu sais que lorsqu'un solide n'est soumis qu'à des forces conservatives, son énergie mécanique se conserve, donc on peut écrire :



soit

Ainsi, au cours des oscillations, l'énergie cinétique se convertit en énergie potentielle et réciproquement.

Et si l'énergie mécanique se conserve : Em = cste => dEm/dt = 0, ce qui fait que tu retrouves l'équation différentielle d'un oscillateur harmonique non amorti trouvée précédemment par la deuxième loi de Newton. En effet, il n'y a pas qu'une seule méthode pour la déterminer.

Une schéma qui pourrait s'avérer utile :



(extrait de )

Avant tout j'avais une petite question qui me bloque a chaque exercice de ce chapitre :
Si au debut on ecarte le ressort de Xo cm quel influence cette variable a sur l'equation differentielle de meme si on lui imprime une vitesse Vo au debut du mvt quel effet cela a sur l'expression de l'equation differentielle ?
Merci !

Qu'est-ce que cela peut influencer ?

Les conditions initiales de la solution de ton équation différentielle.

En effet, tu sais qu'un oscillateur harmonique non amorti a pour solution x = Xm.sin(wo.t + phi) et v(t) = Xm.wo.cos(wo.t + phi).

Si on te précise que x(0) = Xo et v(0) = Vo (valeur numériques)

alors tu peux résoudre le système d'équations

x(0) = Xm.sin(phi) = Xo => équation trigonométrique à résoudre
v(0) = Xm.wo.cos(phi) = Vo => deuxième équation trigonométrique à résoudre

Tu as un exemple traité sur le site fourni (cf. correction, question b)) :

je ne sais comment te remercier vu que je n'ai pas vu cette lecon en classe(mais je l'ai en version pdf et aussi avec le lien de ilephysique de skopps) mais je prend de l'avance pour cartonner
question 5 je n'ai aucune idee car j'ai l'habitude d'exploiter des courbes sinusoidales avec des x en ordonnees mais pas des energies

Je ne comprends pas en quoi c'est problématique : en mathématiques, tu étudies bien des fonctions de la forme f : x --> f(x), avec f(x) de forme hyperbolique, polynomiale, trigonométrique, etc.

Ici c'est pareil avec le paramètre temps t en abscisse : Ep : t --> Ep(t).

Il s'agit d'une lecture graphique comme tu peux le faire en mathématiques pour déterminer le maximum de la fonction, etc.

Tu peux me corriger la premiere question de l'exercice car j'ai ceci :

car dans les conditions initiale on a une vitesse Vo et un allogement Xo ce qui fait que j'ai ceci dans Em(initiale )
J'ai To=0,314s ,Xm=100 , Xo=100

Il faut en revenir à la définition du paramètre "x" :

Energie potentielle élastique : Ep = 1/2*k*x²

Energie cinétique : Ec = 1/2*m*x'²

d'où Em = Ep + Ec = 1/2*k*x² + 1/2*m*x'²

or le système n'est soumis qu'à des forces conservatives, donc l'énergie mécanique se conserve :

Em = constante => dEm/dt = 0

<=> d(1/2*k*x² + 1/2*m*x'²)/dt = 0

<=> k*x' + m*x" = 0

<=> x" + k/m*x' = 0

équation différentielle d'un oscillateur harmonique non amorti x" + wo²*x' = 0

soit une pulsation wo = (m/k)

La solution de l'équation différentielle est de la forme x(t) = Xm*sin(wo.t + phi).

C'est à cette étape que les conditions initiales vont servir, cf. mes messages précédents avec les liens fournis.

Je viens de mieux comprendre les conditions initiales
que dis tu des de mes reponses d'exploitation graphique (appliquant yeux fermes ce que tu as dit )

Quelles réponses d'exploitation graphique ?

Je ne vois rien d'écrit dans ce sujet .

Je te laisse faire l'analyse mathématique et on en rediscute ce soir

tu pars ?

Ce que je voulais te signifier, c'est que tu n'expliques pas ce que tu as fait pour déterminer ces valeurs. Et certaines n'ont pas d'unité

j'ai mesure avec la regle oui certaines n'ont pas d'unites car je ne suis pas de ce que j'ai fait pour les elongations mais pour les periodes je suis confiant

Voici comment j'aimerais que tu rédiges ta réponse :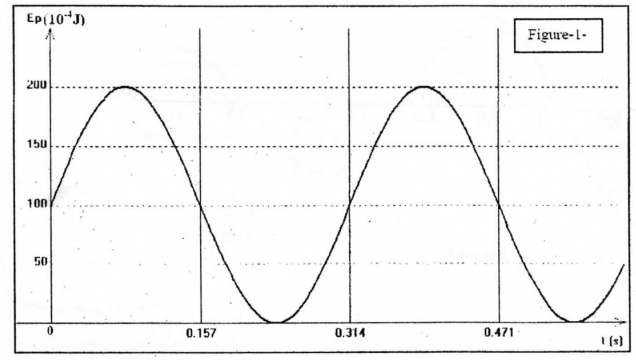







Etant donné que , alors

Ensuite, sachant que l'énergie potentielle élastique est de la forme , une élongation maximale conduit à une énergie potentielle maximale, donc on peut écrire :



etc.

Bonjour gbm , tout d'abord merci de me donner de ton temps .
j'ai ceci : Xmax =2 apres calcul
x(0)=2m alors 2 donc
par lecture graphique la periode propre To=0,314s
wo=
V(0)=20.cos() soit Vo=40m.s
Wo= alors m=
Graphiquement vitesse ou c'est reduit a la moitie , je sais faire ca par calcul mais pas graphiquement

Attention aux unités, ça a un sens physique !

OK pour Xmax (en m), Xo, Phi

Comment as-tu déterminé la période ?

Ok pour Vo mais c'est en m/s

La periode j'ai cherche une portion de courbe symetrique qui se repetait puis j'ai determiner la temps qu'il durait et j'ai 0,314s

Si la période d'oscillation de la fonction x(t) = Xm.sin(wo.t + phi) est To

Est-ce que la période d'oscillation de Ep(t) = 1/2.k.x(t)² est la même ?

Je suis perdu

Relis mon message du 26-04-19 à 21:36 et le lien fourni

***site francophone***