Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Oscillateur harmonique amorti

Posté par
Fina21 21-11-16 à 20:47

Bonsoir tout le monde,
Pouvez-vous me donner des conseils pour résoudre l'exercice suivant:

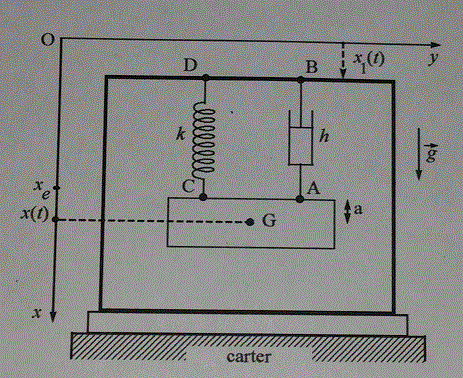
On considère un capteur d'amplitude constitué par un support et une masse m reliés par un ressort et un amortisseur en parallèle.
L'amortisseur exerce en A : \vec{F}A=-h(\vec{v}A-\vec{v}B)
et le ressort en C: \vec{T}c=-k(\vec{DC}-\vec{DoCo})..
Le support, le ressort et l'amortisseur sont de masse négligeable.
Le ressort a pour constante de raideur k et pour longueur à vide lo (notée DoCo).
On suppose que le support est solidaire du carter d'une machine animée d'un mouvement sinusoïdal vertical x1=b\sin \omega t par rapport à un référentiel galiléen  Ro ((Oxy) étant lié à Ro).
1°/ Déterminer l'équation que vérifie xe ( position de la masse à l'équilibre dans Ro lorsque x1=0).
2°/ Ecrire l'équation différentielle du mouvement de m dans Ro.
Si on pose X=x-x1-xe, montrer que l'équation peut se mettre sous la forme :
\ddot{X}+\frac{\omega o }{Q}\dot{X}+\omega o^{2}X=A\sin \omega t


Merci pour toutes vos pistes
  

Oscillateur harmonique amorti

Posté par
vanoisere : Oscillateur harmonique amorti 21-11-16 à 21:42

Bonsoir
Et si tu commencais par poster ce que tu as été capable de faire et ce que tu n'as pas compris?  Ce sera ensuite plus facile de t'aider. L'étude de l'équilibre ne devrait pas te poser de problème.  Ensuite, la relation fondamentale de la dynamique...

Posté par
Fina21re : Oscillateur harmonique amorti 21-11-16 à 22:28

D'accord
pour la question 1, j'ai fait le bilan des forces extérieures:
\vec{P}=mg\vec{i}
\vec{T}C=-k(\vec{DC}-\vec{DoCo})=-k(xe+a-lo)\vec{i}

A l'équilibre la somme des forces extérieures est nulle
je trouve donc que xe=\frac{mg}{k} +lo-a

Ce qui m'embête sur cette question c'est que le résultat proposé est:
xe=\frac{mg}{k}+lo+a

Posté par
vanoisere : Oscillateur harmonique amorti 21-11-16 à 23:00

Dans le cas particulier x1=0, les points Do et D sont confondus. À l'équilibre C occupe une position Ce . xe est l'abscisse du point Ge : position du centre d'inertie à l'équilibre. Ainsi :

\overrightarrow{D_{0}C_{e}}=\overrightarrow{D_{0}G_{e}}+\overrightarrow{G_{e}C_{e}}=x_{e}\cdot\overrightarrow{i}-a\cdot\overrightarrow{i}\quad;\quad\overrightarrow{D_{0}C_{0}}=l_{0}\cdot\overrightarrow{i}

Dans ce cas particulier de l'équilibre, la force exercée par le ressort sur la masse m a pour expression :

\overrightarrow{T_{ce}}=-k\left(\overrightarrow{D_{0}C_{e}}-\overrightarrow{D_{0}C_{0}}\right)=-k\left(x_{e}-a-l_{0}\right)\cdot\overrightarrow{i}

D'où ma condition d'équilibre :

m\cdot g-k\left(x_{e}-a-l_{0}\right)=0\quad;\quad x_{e}=\frac{m\cdot g}{k}+a+l_{0}
Un schéma clair représentant d'une part le ressort à vide et d'autre part le ressort avec la masse m à l'équilibre permettrait de bien comprendre ce calcul un peu formel...
Je te laisse continuer...

Posté par
vanoisere : Oscillateur harmonique amorti 22-11-16 à 02:40

Maladresse de ma part : j'ai supposé les points G et C sur la même verticale ! Il serait préférable d'introduire le point G', de même abscisse que G mais à la verticale de C. Ainsi à l'équilibre :

\overrightarrow{D_{0}C_{e}}=\overrightarrow{D_{0}G_{e}^{,}}+\overrightarrow{G_{e}^{,}C_{e}}=x_{e}\cdot\overrightarrow{i}-a\cdot\overrightarrow{i}\quad;\quad\overrightarrow{D_{0}C_{0}}=l_{0}\cdot\overrightarrow{i}

Posté par
J-Pre : Oscillateur harmonique amorti 22-11-16 à 09:20

Juste pour un peu remuer le bouillon.  

Au repos, l'amortisseur n'exerce aucune force en A (puisque vA et vB sont nulles)

Donc la masse m n'est "soutenue" que par le seul point C.

Pourquoi alors, la masse ne pivote-t-elle pas autour du point C afin de tenter d'aligner sur une même verticale les points C et G ?  ... du moins jusqu'à ce que l'arête inférieure droite de la masse ne cogne sur le fond du support.

Bien sûr on pourrait introduire des guidages sur la masse et ... mais alors pourquoi ne pas l'avoir écrit dans l'énoncé ?

C'était juste pour rire, quoique ...

Posté par
Fina21re : Oscillateur harmonique amorti 22-11-16 à 09:29

Bonjour et merci Vanoise,

Pour la question 2 est-que tu est d'accord avec mon bilan des forces extérieures?
\vec{P}=mg\vec{i}
\vec{T}_{C}=-k(x(t)+x_{1}-x_{e})\vec{i}
\vec{F}_{A}=-h(\vec{v}_{A}-\vec{v}_{B})=-h(\dot{x}-\dot{x}_{1})\vec{i}

Bonne journée!

Posté par
vanoisere : Oscillateur harmonique amorti 22-11-16 à 11:32

Bonjour
Nous sommes d'accord pour dire que l'allongement (pas la longueur) du ressort à l'équilibre est :

\Delta l_{e}=x_{e}-a-l_{0}
Maintenant : regarde bien ton schéma : à la date t quelconque, le ressort s'allonge en C de  \left(x(t)-x_{e}\right) et se raccourcit en D de x1. Dans ces conditions, son allongement à la date t est :

\Delta l=x_{e}-a-l_{0}+x(t)-x_{e}-x_{1}=x(t)-x_{1}-a-l_{0}
Tu peux vérifier que dans le cas particulier de l'équilibre : x1=0 et x(t)=xe, on retombe bien sur l=le
D'où l'expression de la force exercée par le ressort sur la masse :

\overrightarrow{T_{c}}=-k\left(x(t)-x_{1}-a-l_{0}\right)\cdot\overrightarrow{i}
D'accord avec toi pour les autres forces. Je te laisse continuer ; Tu vas devoir commencer par montrer que la résultante du poids et de la tension du ressort s'exprime très simplement en fonction de l'élongation X :

\overrightarrow{T_{c}}+\overrightarrow{P}=-k\cdot X\cdot\overrightarrow{i}
Remarque : il aurait sans doute été plus réaliste de schématiser la suspension par un ensemble de deux ressorts identiques de raideurs k/2, l'un entre C et D, l'autre entre A et B, l'amortisseur étant placé entre les deux, à la verticale de G...

Posté par
Fina21re : Oscillateur harmonique amorti 22-11-16 à 18:54

Bonsoir Vanoise,
maintenant que nous connaissons toutes les forces extérieures, on peut écrire la RFD:\vec{P}+\vec{T'}_{C}+\vec{F}_{A}=m.\vec{a}
on a donc:
m.g-k(x(t)-x_{1}-a-l_{o})-h(\dot{x}-\dot{x}_{1})=m.\ddot{x}

et de là j'ai du mal à poser X=x-x_{1}-x_{e}

Posté par
vanoisere : Oscillateur harmonique amorti 22-11-16 à 19:05

Il a déjà été démontré en étudiant l'équilibre :

m\cdot g=k\cdot\triangle l_{e}=k\cdot\left(x_{e}-a-l_{0}\right)

Dans ton expression de la RFD, remplace m.g par l'expression précédente : tu vas obtenir le résultats que je t'ai indiqué ce matin...
Par ailleurs, en dérivant par rapport au temps l'expression de X, on obtient :

\dot{X}=\dot{x}-\dot{x}_{1}

puisque x_{e} est une valeur indépendante du temps.

Posté par
J-Pre : Oscillateur harmonique amorti 22-11-16 à 19:24

Citation :
Remarque : il aurait sans doute été plus réaliste de schématiser la suspension par un ensemble de deux ressorts identiques de raideurs k/2, l'un entre C et D, l'autre entre A et B, l'amortisseur étant placé entre les deux, à la verticale de G...


Tout à fait.  

Posté par
Fina21re : Oscillateur harmonique amorti 22-11-16 à 22:07

Merci  bcp Vanoise,
Bonne soirée!

Posté par
gbm Webmasterre : Oscillateur harmonique amorti 23-11-16 à 08:29

Bonjour Fina21 :

Pourrais-tu m'expliquer la présence d'un deuxième compte Den242, au risque d'être exclue définitivement pour multicompte ?

Merci.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !