Inscription / Connexion Nouveau Sujet
Oscillateur contraint à ressort
Bonjour,
On considère un point matériel M de masse m se déplaçant sur un cercle de rayon R dans le champ de pesanteur uniforme g=g . On repère la position de M par l'angle
. On repère la position de M par l'angle  =(
=( ,OM).
,OM).
On néglige ici les frottements. Le point matériel est maintenant également fixé à un ressort de longueur au repos l0<R et de raideur k. L'autre extrémité du ressort peut glisser sans frottement sur une tige fixe horizontale confondue avec l'axe Ox. Le ressort reste toujours vertical, se déplaçant uniquement perpendiculairement à la tige. On suppose que la relation mg<k(R-l0) est toujours vérifiée.
1) Faire le bilan des forces qui s'exercent sur le point matériel M.
P le poids, R la réaction du cercle sur la masse et F la force du ressort sur la masse
2) Exprimer l'énergie potentielle Ep totale correspondante à ces intéractions.
Ep = mgR(1-cos( )) + 1/2 * k(R(1-cos(
)) + 1/2 * k(R(1-cos( ))-l0)²
))-l0)²
3) Quelles sont les positions d'équilibres ? S'agit-il d'équilibres stables ou instables ?
C'est là où je commence à douter. Il me semble qu'il faut dériver l'énergie potentielle par rapport à  et lorsque cette dérivée est égale à 0, cela correspond à un équilibre (stable si la dérivée seconde est positive, instable si elle est négative)
et lorsque cette dérivée est égale à 0, cela correspond à un équilibre (stable si la dérivée seconde est positive, instable si elle est négative)
Mais justement je doute de ma méthode car lorsque je fais les dérivées je trouve des formules étranges, est-ce normal ?
On note  =
= c la position d'équilibre stable telle que 0<
c la position d'équilibre stable telle que 0< c<
c< /2
/2
4) Que peut-on dire de la réaction du cerceau à l'équilibre en  =
= c ?
c ?
On donne le développement limité à l'ordre 2 autour de  =
= c de la fonction Ep(
c de la fonction Ep( ) :
) :
Ep( ) = Ep(
) = Ep( c) + dEp(
c) + dEp( c)/d
c)/d * (
* ( -
- c) + d²Ep(
c) + d²Ep( c)/d
c)/d ² * (
² * ( -
- c)²/2
c)²/2
où l'expression diEp( c)/d
c)/d i est une constante, égale à la valeur de la fonction dérivée ième pour
i est une constante, égale à la valeur de la fonction dérivée ième pour  =
= c.
c.
5) Établir l'équation différentielle vérifiée par  pour de petites oscillations de
pour de petites oscillations de  c.
c.
Suffit-il simplement de remplacer dans la formule donnée par l'énonce les Ep et ses dérivées ?
6) Quelle est l'expression générale de la solution de cette équation différentielle ? A quoi correspond le terme k/m * (sin c)² ?
c)² ?
Je n'ai pas encore réfléchi à cette question, j'attends de finir celle d'avant
Merci d'avance pour toute aide !
Salut,
Je suis désolé, je ne pourrais pas te suivre tout au long de cet exercice.
Mais j'ai trouvé un exercice similaire qui pourras très certainement t'aider :
![]()
La grande différence réside dans le fait que
le ressort reste toujours vertical, se déplaçant uniquement perpendiculairement à la tige.
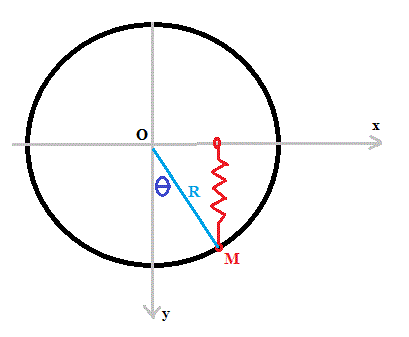
2 à 4)
En prenant le niveau de pour les Epp nulles
Ep = (1/2).k.(R.cos(theta) - Lo)² - mgR.cos(theta)
dEP/dtheta = -k.R.(R.cos(theta) - Lo).sin(theta) + mgR.sin,(theta)
dEP/dtheta = sin(theta) * (mgR - k.R.(R.cos(theta) - Lo))
dEP/dtheta = 0 pour :
a)
sin(theta) = 0 (teheta = 0 ou Pi)
Equilibres instables.
b)
(mgR - k.R.(R.cos(theta) - Lo) = 0
cos(theta) = (mg + k.Lo)/(kR) (qui est toujours possible puisque l'énoncé ptécise que mg<k(R-L0))
theta_c = arccos[(mg + k.Lo)/(kR)]
Equilibres stables
calcul de F ressort à une position d'équilibre stable :
F = -k.(R.cos(theta_c) - Lo)
F = -k.[R.(mg + k.Lo)/(kR) - Lo]
F = -mg - k(Lo-Lo)
F = -mg
La force du ressort sur M compense exactement le poids de M et donc : la réaction du cerceau est nulle à l'équilibre en theta = theta_c.
...
Sauf distraction. 



