Le condensateur est initialement déchargé.

Bonjour
Une méthode possible, peut-être pas encore à ton programme, consiste à étudier le circuit en régime sinusoïdal en utilisant les complexes associés puis à remarquer que multiplier un complexe par est équivalent à prendre la dérivée n^ième par rapport au temps de la grandeur instantanée correspondante. Sinon :



On écrit ensuite que la tension instantanée est commune à C et à {L,R} :



Soit en dérivant :



Cela devrait t'aider pour continuer seul... Poste à nouveau tout de même si tu ne t'en sors pas !

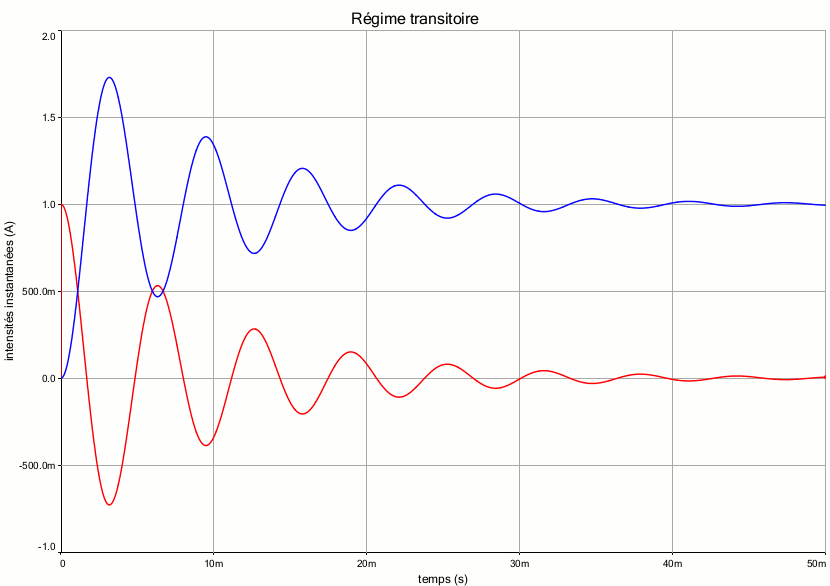
Pour t'aider un peu, voici une simulation représentant en rouge la courbe i₁(t) et en bleu la courbe i₂(t). Fais bien attention en particulier au valeurs initiales et aux valeurs limites quand t tend vers l'infini. J'ai choisi pour le tracé des valeurs totalement arbitraires :
L=0,1H ; C=10µF ; R=20

J'ai oublié une précision : le courant électromoteur fourni pour le générateur idéal de courant a pour valeur dans ma simulation :
I=1A.
J'ai aussi remarqué que l'énoncé note cette intensité I_o plutôt que I... Mais impossible de corrigé les messages déjà envoyés...

Bonjour , c'est déjà très gentil à vous d'avoir répondu !
Cependant une petite incompréhension persiste :
Vous faites apparaître q(t) pour le dériver et ainsi faire apparaître une intensité. Pourquoi cette intensité est et pas une autre intensité du circuit ?

Ouch non c'est bon c'était évident.

Merci beaucoup, je vais maintenant essayer de résoudre l'équation.

Peut-on considérer le second membre nul. Je ne pense pas mais sinon ce serait terriblement long... il faudrait aussi trouver une solution particulière...

La solution générale est effectivement la somme de deux solutions :
1° : la solution particulière correspondant au régime permanent ; simplissime : il suffit de considérer toutes les dérivées comme nulles dans l'équation différentielles : i_2p=I_o
2° : la solution homogène i_2h : solution de l'équation différentielle dans le cas où I_o=0 (second membre de l'équation nul). Là : tu as trois types de solutions possibles selon les valeurs de R,L et C. Le cas que j'ai illustré précédemment correspond à une résistance suffisamment faible pour obtenir un régime pseudo-périodique. Cette étude est sûrement détaillée dans ton cours. Sinon, tu peux consulter la fiche n° 10 ici :

L'exemple étudié est un peu différent de celui qui t'intéresse mais l'adaptation est facile me semble-t-il.

Dans mon cours il y a des pages et des pages pour trouver la solution particulière. C'est justement là ou les complexes interviennent.

Ah mais mais le second membre dépend du temps.. ce qui n'est pas notre cas ici.. soit je vais surement trouver maintenant merci

Super !
Je te laisse travailler !
Pourrais-tu fournir les valeurs numériques de R,L,C et I_o ?

Bien sur

J'ai donc résolue l'équation en remplacant dans l'équation la solution admise ceavec r un nombre complexe, à priori. Ce qui me donne en développant une équation du second degré. On calcule le discriminant.
(Sachant que j'ai posé Q et Oméga(O) précédemment (facteur de qualité et pulsation) , je trouve que Q = 5 , ce qui est supèrieur à la valeur critique 0,5). Le discriminant est donc négatif.  

Il y a donc deux solutions complexes. La solution générale est une combinaison linéaire des deux solution + .
Je dois maintenant déterminer les constantes...

Le hasard fait bien les choses : les valeurs numériques que j'ai choisies pour tracer les courbes correspondent aussi à Q=5... mais j'ai choisi Io=1A au lieu de 5A...

Donc ça voudrait dire que à l'instant t=0+ ,

je voulais dire

Mais c'est possible que le condensateur reçoive une intensité supérieure à celle fournie par le générateur comme le montre le graphique ?

La courbe en bleu correspond à l'intensité du courant traversant la bobine.
La contrainte physique est i₁+i₂=I_o
Lorsque l'intensité du courant dans la branche du condensateur est négative, l'intensité du courant à travers la bobine est supérieure à I_o.

Ok merci !

Encore des petites choses ! Avec quoi ou quel logiciel avez vous construit les courbes ?

Et secondo, à votre avis il existe une ou deux constantes à déterminer ? Il y en aurait deux selon mon cours, mais seulement une condition initiale..

Tu n'as pas bien observé les courbes...
De façon générale une inductance assure la continuité de l'intensité dans sa branche alors qu'un condensateur assure la continuité de la tension à ses bornes. Donc ici  :
à t=0+ : i2=0 ; i1=Io-i2=Io  ; u=0.
Je te laisse montrer qu'à la même date, la dérivée de i2 par rapport à t vaut zéro.
Je suppose qu' avant la fermeture de l'interrupteur le condensateur est déchargé et la bobine traversée par aucun courant.

Ne faudrait-il pas montrer que q(t) à t=O+ est nul ducoup ?

J'ai déjà en grande partie répondu à tes interrogations.
Le condensateur assure la continuité de la charge donc la continuité de la tension u à ses bornes. Donc à t=O+ :


Or, la bobine assure la continuité de l'intensité du courant dans sa branche :

à t = 0+ : i₂=0

On obtient donc à t = 0+ :



Les voila les deux conditions particulières qui vont te permettre d'obtenir l'expression de i₂(t)...

Je trouve que la solution s'écrit avec to et w  des éléments que l'on a posé pour simplifier l'expression .

donc

Et dans l'hypothèse que la dérivée est nulle,  je trouve que

A vu d'oeil pouvez me dire si ça pourrai être cohérent ?

Ah ok en fait la dérivée de i est nulle car i est nulle ... tout simplement merci !

1. Lorsque tu as posté à 19h53 tu n'avais sans doute pas lu mon message de 19h51. J'y démontre que di2/dt est nul à t=0+ parce que, à cette date,  i2  et u  sont nuls.
2. D'accord avec ta valeur de B1.
3. Tu obtiens une valeur de B2 homogène au produit d'une intensité par le carré d'un temps  : nécessairement faux;  B2 a la dimension d'une intensité. Revois ton calcul;  tu devrais aboutir à B2=0...

Erreur à la dernière ligne de mon précédent message . B2 n'est pas nul et dépend bien de Io et de t_o mais le point no2 de mon précédent message reste valide.

Bonjour
Je n'ai pas été très clair hier soir sur l'expression de B2. Je reprends. Si tu écris l'expression de la solution générale sous la forme :



La condition particulière conduit comme tu l'as écrit à : . L'expression générale de la dérivée par rapport au temps est :



Cette dérivée est nulle à t=0+ :



Soit :



B2 a bien la dimension physique d'une intensité !

Ayant ainsi obtenu , tu obtiens facilement i1(t) :

Ok ça marche. Merci beaucoup pour le calcul de dérivée. En plus j'avais fait une grossière erreur mais je retrouve finalement la même chose que vous.
Donc pour récapituler on trouve


Je reviens à l'expression de mon premier message où j'ai déterminé l'expression de i1.

Je trouve que la dérivée de est :

D'accord avec tes résultats. Tu as sûrement constaté que di₂/dt vaut zéro en t=0...

Super merci !
hum oui.. c'est ainsi que nous avons déterminé la constante B2..

Bravo à vous ! C'est super de pouvoir compter sur des gens comme ça !

Puis-je vous poser une autre question indépendante de l'exercice ?

Puis-je vous poser une autre question indépendante de l'exercice ?

Pourquoi pas. Tu peux aussi créer un nouveau topic pour cela.

Bon ça devrait aller. Ce serait trop long et compliqué à expliquer. En tout cas merci beaucoup !!!

Bonne soirée