Inscription / Connexion Nouveau Sujet
Oscillateur amorti - Puissance instantanée
Bonsoir à tous,
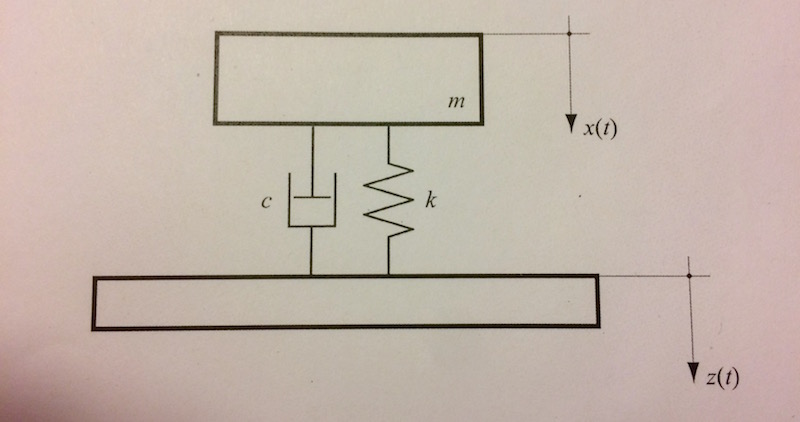
Dans un exo de méca vibratoire, on demande de calculer la puissance instantanée du système ci-dessous. Où c est la résistance de l'amortissement et k la rigidité du ressort.
On fait vibrer la table tel que z(t)=Zcos(
t) et le mouvement de la masse est désigné par x(t) = Xcos(t -
).
J'obtiens pour l'équation de mouvement :
Cependant je ne parviens pas à obtenir l'expression de la puissance instantanée.
Selon moi c'est la vitesse fois la force, mais ça ne m'avance guère. Y-a-t-il une formule qui ne me saute pas aux yeux pour la puissance? avec ce terme au carré cela me perturbe.
Le corrigé nous dit que
Auriez-vous une idée de comment il obtient cela ?
Merci à tous
Bonsoir
La force exercée par le ressort est de la forme : k(z-x) : je te laisse réfléchir à la question : s'agit-il de la force exercée par le ressort sur la masse m ou de la force exercée par le ressort sur la table ? Bien sûr : il s'agit de deux forces opposées dans la mesure où la masse du ressort est d'influence négligeable.
DE même, la force exercée par l'amortisseur est de la forme : c(x' - z') ; là encore, je te laisse gérer les problèmes de signe... Pour la puissance de la force exercée par l'amortisseur, la puissance fait intervenir le produit de la force par la vitesse relative (x'-z')...
Merci pour la réponse,
Alors f=k(z-x) est la force exercée par le ressort sur la masse, et la force exercée par l'amortisseur sur la masse est f=c(z'-x') non ?
D'accord pour le vitesse relative mais je ne vois pas pourquoi il y a ce terme au carré ?
Est-ce la formule de la puissance instantanée pur un oscillateur amorti ?
p(t)= cy' avec y' vitesse relative de l'oscillateur par rapport à son référentiel ?
Annuler
connectez vous