Inscription / Connexion Nouveau Sujet
oscillateur amorti
Bonjour,
je cherche de l'aide pour un exercice sur lequel je bloque complètement. Merci à l'avance si quelqu'un peut m'aider.Le voici:
On considère le pendule élastique d'axe horizontal Ox constitué d'un point matériel de masse m relié à un point fixe A du référentiel terrestre par l'intermédiaire d'un ressort de raideur k. Il existe une force de frottement solide entre le point et son support horizontal.
On suppose qu'elle obéit aux lois de Coulomb avec un facteur de frottement dynamique 
(que l'on suppose égal au facteur de frottement statique f).
A l'instant initial, on lâche sans vitesse le point matériel à l'abscisse x0 strictement supérieur à 0(la longueur du ressort est égale à sa longueur à vide à l'abscisse x=0).
1)Déterminer l'équation différentielle du mouvement. On pose T0=2
(m/k).
Calculer x(t) pour t appartenant aux intervalles: [0,T0/2], [T0/2T0],[T0,3T0/2],..., puis [nT0,(2n+1)T0/2] et [(2n+1)T0/2,(n+1)T0] tant qu'il y a mouvement . Quel est le signe de x° sur ces 2 derniers intervalles ?
2) Déterminer les abscisses extrémales xmax et xmin du point matériel au cours du mouvement, en fonction du nombre n d'allers et retours effectués, ainsi que l'équation des courbes Xmax (t) et Xmin (t) reliant les points correspondant à ces extrémums dans le plan (t,x).
Justement, pas grand chose. JE ne connais pas la loi de Coulomb avec un facteur de frottement dynamique et je ne vois pas ce qu'on demande par l'équation différentielle du mouvement en posant T0.
Comme pour l'autre exo qu'on avait fait ensemble :
* système :
* référentiel :
* Bilan des forces :
Pour rappel, la loi de Coulomb est : 
Système : point matériel de masse m
Référentiel : terrestre supposé galiléen
Repère : Ox
Actions extérieures : A distance : Terre sur point : poids : vecteur P = m vecteur g
De contact : Support sur point : vecteur R = vecteur N + vecteur T avec ||vecteur T||=f||vecteur N||
Je suppose que c'est ça jusque là, mais il me manque l'action du ressort,non?
Bonjour, excuse-moi pour hier mais j'ai quitté l'île à ce moment là...
Oui il faut ajouter la force de rappel exercée par le ressort.
Ensuite, applique la deuxième loi de Newton (ou PFD)
Force de rappel: vecteur F= -k(l-lo) vecteur Ox. C'esr ça
PFD: vecteur P+vecteur N+vecteur F=m vecteur a
Projection sur Ox: 0+f*RT-k(l-lo)=m (dv/dt)
0+T0-k(l-lo)= m (dv/dt)
To/m -k/m(l-lo= (dv/dt)
[2(m/k)]/m -k/m(l-lo)=(dv/dt)
Ce serait ça l'équation différentielle?
Comment faire la deuxième partie de la question?
0+f*RT-k(l-lo)=m (dv/dt)
0+T0-k(l-lo)= m (dv/dt)
je ne comprends pas ton passage, tu as dit que T = fN (la réaction du support s'oppose au dépacement..)
OUPS
Alors: Projection sur Ox:0+f*RN -k(l-lo)=m (dv/dt)
0+T0-k(l-lo)= m (dv/dt)
To/m -k/m(l-lo= (dv/dt)
[2(m/k)]/m -k/m(l-lo)=(dv/dt)
C'est ça l'équation différentielle?
Si oui, comment faire la deuxième partie de la question? car là, j'avoue que je nage.
0+T0-k(l-lo)= m (dv/dt)
pourquoi tu remplaces f.Rn (ou fN) par To ?? qui est une période ???
de plus si Ox est dirigé vers la droite il y a une erreur de signe ...
T
Tu confonds T la réaction tangentielle (N est la réaction normale du support) et T la période des oscillations !
Alors: Projection sur Ox:0-f*N -k(l-lo)=m (dv/dt)
0-RT-k(l-lo)= m (dv/dt)
-T/m-k/m(l-lo)= (dv/dt)
Comment fait-on intervenir T0 alors?
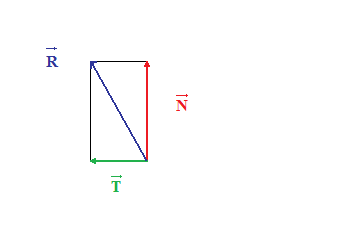
Souviens-toi de la réaction du support untilisée en première ou terminale, on négligeait les frottements. Ici on le fait intervenir donc et en projection sur les axes, on a
et
avec en norme T = fN
vecN c'est
Le To intervient par la suite.
0-f*N -k(l-lo)=m (dv/dt)
ok
ensuite comme en terminale, on assimile l-lo à x
l'équation devient
(en faisant tout passer dans le membre de droite)
Alors: d^2x/dt^2+(k/m)x+(f/m)N=0
Ce serait donc l'équation différentielle.
Il faudrait donc trouver x maintenant. Mais je ne sais pas trop comment m'y prendre. Désolée, je suis vraiment nulle.
Alors il faut aussi que je projette sur un axe Oy?
OUI TB ! cela peut te donner une valeur de N (car on ne l'a pas dans l'énoncé).
En supposant Oy dirigé vers le haut :
-mg + N = 0 <=> N = mg (tu as des idées donc tu n'es pas nulle
)
Bref tu obtiens une équation différentielle du deuxième ordre à coefficients constants.
Méthode classique :
* équation caractéristique
* résolution
*...
Alors, on obtient l'équation différentielle suivante:
d^2x/dt^2+(k/m)x+(f/m)*(mg)=0
d^2x/dt^2+(k/m)x= -(f/m)*(mg)
d^2x/dt^2+(k/m)x= -fg (équation différentielle du deuxième ordre à coefficients constants)
Equation caractéristique:x^2+k/m+fg=0
=-4(k/m)-4fg
Mais j'avoue qu'après je ne sais plus. Quelqu'un pourrait-il m'aider s'il vous plait?
Re marissa 
d^2x/dt^2+(k/m)x= -fg
TB ! Cette équation a donc un second membre !
Méthode :
* solution homogène :
On résout
qui est de la forme classique
avec
donc
(ouf on retrouve To !)
Donc la solution de l'équation homogène est x(t) = Acos(wot) + Bsin(wot)
* solution particulière :
il faut ensuite trouver une solution xp (c'est une constante) particulière qui vérifie l'équation
Merci beaucoup gbm.
pourrait tu s'il te plait m'aider pour trouver la solution particulière car malheureusement sur ça aussi je bloque.
Il faut trouver xp tel que
d^xp/dt^2 + k/m xp = -fg
xp = constante donc k/m xp = -fg
soit xp = -(fgm)/k
semble convenir (à vérifier)
Ensuite il faut que tu utilise les conditions initiales pour avor A et B
Merci gbm, je calculerai demain soir parce que là j'ai eu colle jusqu'à 8H. Quoi que demain c'est jusqu'à 7H, mais enfin j'essayerai quand même.
Bonne soirée et à demain si je peux. Merci encore.
Annuler
connectez vous