Inscription / Connexion Nouveau Sujet
Oscillateur à modulation de fréquence
Bonsoir !
J'érpouve quelques, comment dirai-je, difficultés à résoudre un exercice de physique qui consiste à étudier un oscillateur à modulation de fréquence.
Pour le réaliser on branche une diode à capacité variable en parallèle avec la bobine d'inductance L. On assimile cette diode à un condensateur dont la capacité C(s) est fonction d'une grandeur s, susceptible de changer avec le temps. C(s) varie selon la loi C(s)=Asn où A et n sont des constantes positives.
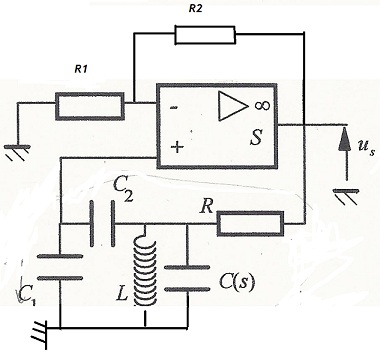
On réalise le montage qui suit.
Etablir la fonction de transfert H(jw)=1/(a + 1/(bjw) + djw) en explicitant a, b et d en fonction de C(s), R, L, C1 ,C2 Ca je pense avoir réussi j'ai trouvé a = 1 +C1/C2, b = LC2/(RC2 - C1) et c = C1 + C1C(s)/C2 + RC(s)
Mais dès la question suivante je suis un peu larguée.
On considère le montage 2. On fixe s à S0 et ainsi C(s) = C0. Exprimer la pulsation 
0 de l'oscillateur spontané en sortie en fonction de C0 ,L ,C1, et C2. Expliquer ensuite par le biais d'une équation différentielle que la condition de naissance des oscillations est en fait une inégalité à écrire.
Ensuite il y a d'autres questions que je viendrais peut-être poser par la suite. Mais pour le moment mon problème c'est comment démarrer pour trouver l'expression de 0 parce que je n'ai strictement aucune idée. Pour ce qui est de la condition de naissance d'oscillations sinusoïdales je pense qu'il faut passer la fonction de transfert en temporel pour trouver la condition (le signe de la dérivée du premier ordre) mais comment utiliser mon résultat d'avant dans ce montage ?
Enfin voilà, toute aide et piste est la bienvenue... Merci =)
Bonjour,
Je vais vérifier pour la première question.
Pour la deuxième, ce sont des conditions sur la fonction de transfert.
Pour qu'il y ait oscillation, il faut que la tension réinjectée sur l'entrée + soit en phase avec us (parce que c'est l'entrée +). Ceci revient à dire que la partie imaginaire de la fonction de transfert doit être nulle.
De plus, le gain global de l'étage à ampli op doit être supérieur à 1.
Dit comme ça, c'est peut-être un peu obscur...
Il faut, en fait, couper fictivement le circuit à l'entrée +. En injectant une tension sur l'entrée +, on calcule alors la tension sur la sortie du circuit (aux bornes de C1) et on doit avoir la phase nulle et le gain 
1.
Tous les oscillateurs se calculent comme ça.
Bonsoir !
Oui en fait je me suis trompée, j'ai vérifié avec mon professeur et j'avais rectifié.
Donc pour les coeff c'est OK
Pour après j'ai écris v1=us, v2= (R1/(R1+R2))us et v2=Hv1 et en mixant tout ça j'ai v2(1-H(R1+R2/R1)=0
On peut avoir v2 non nul si H(R1+R2/R1)=1 et j'ai trouvé une condition R1C1=R2C2 et =1/
bd
Ca revient au même que ce que vous proposiez non ?
Annuler
connectez vous