Inscription / Connexion Nouveau Sujet
ordre de réaction et représentation graphique (8)
Bonjour à tous,
Je poursuis dans les exercices de chimie générale.
Je rencontre de nouveau un petit soucis dans la détermination de l'ordre.
Voici l'énoncé:
"Soit la réaction C3H7Br + S203² ---> (réaction partielle) C3H7S2O3 + Br⁻
La concentration en ion thiosulfate a été déterminée en fonction du temps par titrage avec l'iode. Nous obtenons les résultats suivants:
t(en sec) [S2O3²-] (en mM)
0 96,6
1110 90,4
2010 86,3
3192 81,9
5052 76,6
7380 72
11232 66,8
78840 57,1
La concentration initiale en C3H7Br = 39,5 mM
On nous demande de déterminer l'ordre de la réaction puis d'en déterminer la valeur de la constante cinétique."
Pour commencer il semble judicieux d'effectuer un tableau d'avancement
C3H7Br + S203² - --> C3H7S2O3 + Br⁻
t= 0 ni(1) ni(2) 0 0
t ni(1)-x ni(2)-x x x
A partir de là nous pouvons supposer V = 1L
Et déterminer x
Puisque [S2O3²-]t = [S2O3²-]i - C soit C = [S2O3²-]i - [S2O3²-]t
Par ailleurs lorsque nous avons déterminer C il nous est désormais possible de déterminer [C3H7Br]t = [C3H7Br]i - C
Ensuite pour déterminer l'ordre de la réaction, nous devons confirmer soit l'hypothèse que ln([A]/[A]o) en fonction de t est linéaire soit l'hypothèse que 1/[A] est une droite affine.
Nous pouvons compléter le tableau suivant (image).
Cependant après avoir déterminer les graphiques, je ne parviens pas à conclure sur les hypothèses car aucun des 2 graphe ne respecte pas la linéaire.
Quelqu'un aurait la gentillesse de m'aiguiller?
Merci par avance.
Mimi
Bonsoir
Puisque tu as montré que l'ordre n'est pas égal à 1, il faut tester l'hypothèse d'un ordre partiel égal à 1 pour chacun des deux réactifs. La méthode est plus compliquée que ce que tu as fait car le mélange initial n'est pas stoechiometrique. Reprend la définition de v et intègre.
Pour être un peu plus précis, tu peux remplir directement un tableau en raisonnant sur les concentrations :
| espèces chimiques | C3H7Br | S2O32- | C3H7S2O3 | Br- |
| concentrations initiales | c1 | c2 | 0 | 0 |
| concentrations à la date t | c1-c | c2-c | c | c |
Si l'hypothèse d'un ordre partiel de 1 pour chaque réactif est vérifiée, alors :
Je te laisse intégrer. Petit indice tout de même d'ordre mathématique : tu as sans doute démontré en cours de math :
Cela devrait t'aider pour l'intégration...
Merci Vanoise pour ta réponse, mais je suis totalement perdue!! Je ne comprends pas quelle fonction usuelle utilisée d'autant que j'ai énormément de mal avec les primitives!
Bonjour
Je pars de l'équation différentielle fournie dans mon message du 29/11 à 17h14 :
On sépare les variables :
En remarquant (voir cours de math) :
On obtient :
On intègre :
Cas particulier de l'instant initial :
Donc :
ou encore :
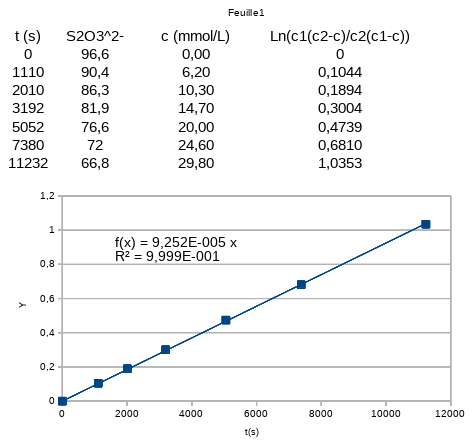
Il suffit de placer dans un repère les points de coordonnées . Si on obtient des points alignés correctement avec l'origine du repère, on pourra conclure à la validité de l'expérience et on pourra déterminer la constante de vitesse puisque le coefficient directeur de la droite moyenne vaut :
.
Voici le résultat obtenu avec un tableur.
Remarque : je 'ai pas tenu compte du dernier point expérimental ; il correspond à une date presque 8 fois plus grande que la précédente et surtout, il correspond à c=c1 : dans ce cas, la vitesse est nulle et évidemment le tableur retourne un message d'erreur au calcul du logarithme. Le concepteur de l'énoncé a sans doute voulu indiquer qu'au delà de cette date, on peut considérer la réaction comme terminée mais cela n'est pas judicieux : la réaction ne s'arrête pas brutalement à une date donnée. La valeur de c tend asymtotiquement vers c1 et au delà de cette date, la courbe c=f(t) est pratiquement confondue avec l'asymptote horizontale c=c1.
vilain lapsus de ma part quand j'écris : "Si on obtient des points alignés correctement avec l'origine du repère, on pourra conclure à la validité de l'expérience"
Je rectifie : "Si on obtient des points alignés correctement avec l'origine du repère, on pourra conclure à la validité de la théorie".
En sciences : l'expérience à toujours le dernier mot, pas la théorie !
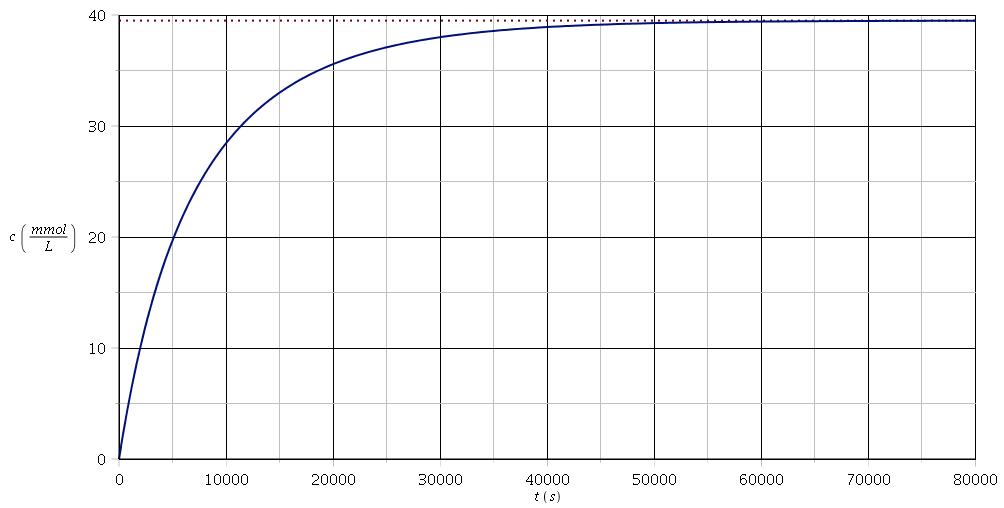
Pour illustrer la remarque de mon message du 01-12-17 à 12:04 sur le comportement asymptotique, voici la courbe c = f(t) déduite de la relation :
On voit bien que c tend vers c1=39,5mmol/L et que, pour t plus grand que 60000s environ, la courbe est pratiquement confondue avec l'asymptote.
Bonsoir,
Un très grand merci Vanoise pour les explications. 
Je comprends davantage.
Et me rends compte que si je ne maîtrise pas les primitives, je serai totalement perdue.
Je viens de reprendre l'exercice.
Je ne comprends pas comment déterminez vous: "le coefficient directeur de la droite moyenne vaut : K=(c2-c1).k"
Si nous confirmons l'hypothèse que la réaction est d'ordre global = 2
v = k.[A]² (avec l'intégration précédemment faite)
nous obtenons
k = ln([C1(C2-C)]/[C2(C1-C]) / (C2-C1)t
Ainsi donc, par exemple,
à t = 2010s
C1 = 29,2 mM
C2 = 86,3 mM
C = 10,3 mM
Donc k = ln([29,2(86,3-10,3)]/[86,3(29,2-10,3]) / [(86,3-29,2) x 2010]
k = 2,68.10⁻6

Si nous confirmons l'hypothèse que la réaction est d'ordre global = 2
v = k.[A]² (avec l'intégration précédemment faite)
Pas ici : l'ordre global égal à 2 correspond à v=k.[A].[B] ; ce n'est pas la même chose dans la mesure où les concentrations initiales des deux réactifs sont différentes.
Concernant les points expérimentaux maintenant :
pour t = 2010s : ln(c1(c2-c)/c2(c1-c)=0,1984 ; K=0,1894/2010=9,422.10-5s-1
Je prends un autre point expérimental au hasard :
t=7380s : ln(c1(c2-c)/c2(c1-c)=0,6810 ; K=0,1894/7380=9,228.10-5s-1
Compte tenu des erreurs inévitables sur les mesures, les points expérimentaux ne sont pas rigoureusement alignés avec l'origine ; les valeurs de
On en déduit la valeur moyenne de la constante de vitesse :
ou si tu préfères : k
 1,62.10-6L.mmol-1.s-1
1,62.10-6L.mmol-1.s-1

