pas sure du tout mais tu dois certainement avoir une équation du type x²/a²  +y²/b²=1 pour une trajectoire elliptique et x² +y² = r² si c'est un cercle  mais tu n'as rien de plus dans ton énoncé ?

Je n'ai pas d'énoncé, je me demandais juste si c'était possible de connaître la trajectoire d'un projectile autour de la planête avec des données initiales dans un énoncé, comme par exemple l'accélération donné à la balle par le canon.

je sais qu'une des relations essentiel en gravitation est F= - G*m*M/r²

il me semble qu'avec un bilan energetique tu peux savoir la trajectoire

en passant par l'énergie mécanique
Em=Ec+Ep

Em=1/2 m *r'² +1/2 m * c²/r²-k/r=constante
constante car F est un potentielle newtonien donc conservatif
1/2 m *r'² étant l'energie cinétique radiale
et 1/2 m * c²/r²-k/r l'énergie potentielle effective
C est la constante des aires

si k<0 tu auras une hyperbole
k>0 tu as 4 cas possible

Em>0 tu auras une hyperbole
Em=0 tu auras Ec=-Ep, une parabole
Em>0 et Em>-k/4r tu auras une ellipse
Em=Ep/2 tu auras une trajectoire circulaire.

sans énoncé je ne saurais faire réellement mieux^^

En "oubliant" les frottements :

Avec h l'altitude du tir (supposé horizontal), on a :

Trajectoire circulaire si : GmM/(Rt + h)² = m.v²/(Rt + h)

v² = GM/(Rt + h)

v = racinecarrée[GM/(Rt + h)]

avec v la norme de la vitesse du boulet, G la constante de gravitation, M la masse de la Terre, (Rt + h) le distance entre le centre de la Terre et le boulet au moment du tir.
---
En appelant Vo la vitesse du boulet au moment du tir, on a :

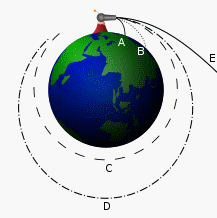
Si Vo < racinecarrée[GM/(Rt + h)], on a des trajectoires du style A et B ( paraboliques avec crash sur la Terre)
Si v = racinecarrée[GM/(Rt + h)], on a une trajectoire circulaire (style C) à l'altitude h.
Si v > racinecarrée[GM/(Rt + h)] mais < que la vitesse de libération, on a une trajectoire elliptique type D.
Si v >= vitesse de libération (soit v >= racinecarrée[2GM/(Rt + h)]), on a une trajectoire type E ... le boulet échappera à l'attraction de la Terre. (trajectoire hyperbolique).
---

C'est évidemment faux si on tient compte des frottements air-boulet.

-----

Calcul de la vitesse de libération :
Le projectile échappe à l'attraction terrestre (hors frottement) si son énergie cinétique au moment du lancer est suppérieur à l'énergie qu'il faut pour que le projectile atteigne l'infini.

On a alors : (1/2).m.V² >= GmM/(RT+h)
V >= racinecarrée[2GM/(Rt + h)])
La vitesse de libération est VL = racinecarrée[2GM/(Rt + h)])
-----
Sauf distraction.  

Merci, j'ai pu faire le lien entre votre réponse et mon cours. C'est en effet ce sur quoi je travaille actuellement