Inscription / Connexion Nouveau Sujet
Optique,oppm et interférences.
Bonsoir à tous,
Je voulais savoir si mes réponses étaient bonnes pour l'exercice qui suit:
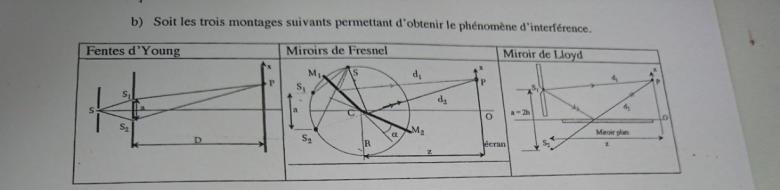
a)Soit les montage suivant permettant d'obtenir le phénomène d'interférence .
En fonction des caractéristiques géométrique de chaque montage sur les figures précédentes,donner la formules de l'interfrange i pour chacun des montages.
b) énoncé les trois propriété fondamentales de l'onde plane progressive monochromatique électromagnétique(OPPM).
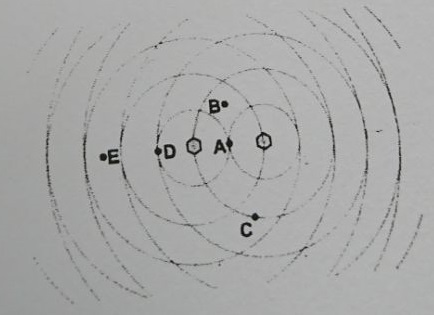
c)Sur la figure ,chaque cercle représente un front d'onde (crête maximum d'amplitude).
Dites s'il y a interférence destructive ou constructive aux points A,B,C,D,E?
Voici mes réponses:
Pour la fente de Young je sais que l'interfrange après le reste j'ai pas encore trouver sur le net ou dans mes cours.
b)Je connais des choses,mais les 3 propriétés...
Je sais que l'OPPM est une onde,plane,progressive(elle évolue dans le temps et l'espace),et est monochromatique(une seule longueur d'onde donc une seule fréquence).
Une Onde est dite Plane si à un instant t donné, la grandeur
qui caractérise l'onde qui se propage est la même en tous les points d'un plan
perpendiculaire à la direction de propagation de l'onde.
Une Onde Plane Progressive est une onde plane qui se propage
dans un sens et une direction bien déterminés
c) interférences constructives : c'est les point A et B ( tous les points qui forment une droite). Les deux cercles(qu'importe leur taille) étant symétriques par
rapport à cette droite.
Ainsi les points E,D,C ne sont pas constructif.
Bonsoir
Tout va bien sauf pour pour la dernière question. Revois bien ton cours. En supposant les deux sources vibrant en phase, il y a interférence constructive en un point donné si les deux ondes qui y interfèrent sont en phase ; cela suppose une différence de marche entre les deux ondes progressives (différence des distances aux deux sources) multiple de la longueur d'onde :
d2 - d1 = k.
où k est un entier relatif : k
.
Il y a interférence destructive en un point donné si les deux ondes qui interfèrent en ce point sont en opposition de phase : cela suppose une différence de marche de la forme :
d2 - d1 = (k+1/2). où k est un entier relatif : k.
Salut vanoise,j'espère que t'a passé de bonne fête.
Sinon,si j'ai compris,le plus petit cercle a pour rayon donc les point A et D se situent à k.
k étant ici égal à 1 ou -1.
Pour B on est à la moitié du second cercle donc c'est pas un nombre entier(3/2 ou -3/2).
E on est à 5/2 ou -5/2.
Et C c'est un nombre entier( k= 2 ou -2 ).
Donc pour A,D,C on a une interférence constructive,et pour B et E c'est desctructif?
En gros tant qu'un point est sur un des cercle,c'est constructif.(pour 2 source en phase),si c'est déphasé,autre histoire...
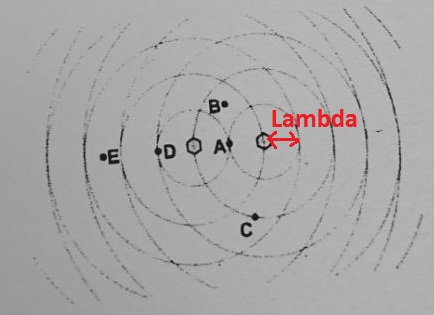
En gros tant qu'un point est sur un des cercle,c'est constructif
Faux ! Tu n'as pas compris mon précédent message !
Si un point appartient à un cercle, une des deux distances est un multiple de
; cela ne signifie pas nécessairement que la différence des distances aux deux sources est multiple de !
Exemple du point C : d1=2,5
; d2=2 ; d1-d2=/2 : interférence destructive !
De même, si un point est entre deux cercles, une des distance est de la forme (k+1/2)
mais la différence des distances peut être multiple de ou nulle. Exemple : le point B : d2=d1=1,5. d2-d1=0 : interférence constructive !
Réfléchis bien à tout cela !
Annuler
connectez vous