Bonjour,

Tu peux déjà lire ceci : optique

j'ai toujours rien compris, en cours on n'a pas vu l'optique

Quelles sont tes réponses aux premières questions ?
J'en ai besoin pour savoir ce que tu as compris et ce qu'il faut approfondir.

1) une lunette astronomique est constituée de 2 lentilles : l'objectif et l'oculaire. Dans ce cas, l'objectif est la lentille qui a la plus grande ditance focale donc L1 est l'objectif et l'autre lentille joue le rôle d loupe placé devant l'oeil c'est alors l'oculaire.
2)la lunette astronomique étant réglée pour être afocaledonne à l'oeil une image de l'infini sans que l'oeil fatigue et qu'il est une vision net de l'infini.

Très bien !

1)
Puisque l'image de l'objet "à l'infini" (la Lune...) se formera dans le plan focal image de la première lentille, que l'on veut une image aussi grande que possible, que la taille de cette image est f'₁ pour un objet de diamètre apparent , on a intérêt à avoir une distance f'₁ aussi grande que possible
Donc : l'objectif est la lentille avec la distance focale la plus grande possible.

Cette image est regardée avec l'oculaire qui est utilisé comme une loupe. Une loupe grossit d'autant plus qu'elle a une distance focale courte.
Donc : l'oculaire est la lentille avec la distance focale la plus petite possible.

2)
Oui, c'est, pour un œil normal, quand l'image est à l'infini qu'il peut la regarder sans fatigue. C'est l'intérêt du réglage "afocal" : l'image intermédiaire est dans le plan focal image de l'objectif qui est confondu avec le plan focal objet de l'oculaire ; l'image donnée par l'oculaire est alors à l'infini.

3)
J'ai fait un schéma dans l'autre topic...

4)
Avec ce que j'ai écrit plus haut (pour la réponse à la première question) et avec le schéma, que peux-tu répondre aux questions 4a) et 4b) ?

chui pas sur est-ce que le rayon de l'image intermédiaire serait pas égale à celui du rayon initial donc alpha=alpha'

Je remets l'image pour la commodité :



L'angle sous lequel le rayon de la Lune est vu à l'œil nu est

L'angle est aussi l'angle puisque les rayons qui passent par le centre d'optique d'une lentille (ici l'objectif) ne sont pas déviés.

Tu connais la distance OA'

Il est facile d'en déduire la taille de l'image intermédiaire A'B'

N'oublie pas qu'en optique géométrique (ici, dans l'approximation de Gauss) on travaille avec de très petits angles et qu'en conséquence à condition d'exprimer en radian on peut confondre
tan() avec sin() et avec (en radian)

aaaaaaaaahhhh!!!!!!!!! d'accord g compri merci bocoup

Peux-tu (en pensant aux suivants par exemple...) poster tes réponses ?
De plus je les vérifierai

4a) Soit B, un point de la circonférence de la lune alors alpha= angle A'OB'=angle AOB= 4.4*10^-3 rad
A'B' = 4.5*10^-1 m (chui pa sur que ce soit ca :?)

A'B' = OA' . tan()
et donc
A'B' OA' .
en exprimant en radian

Où se trouve l'image intermédiaire A'B' par rapport à l'objectif ? Que vaut donc la distance OA' ?

bonjour coll
j'ai moi aussi le meme exercice sur la lunette astronomique et je n'arrive pas a faire le shema qui est demandé.
pourrais tu m'aider stp ?
merci d'avance.

Bonjour rébecc,

Le schéma demandé ressemble beaucoup, je pense, à ce que j'ai posté le 19 août à 17 h 43 (message 1221581)

Je n'ai pas indiqué sur ce schéma la position des foyers.

Peux-tu dire où doit se trouver, sur ce schéma, le foyer image F'₁ de l'objectif et où doit se trouver le foyer objet F₂ de l'oculaire pour que la lunette soit réglée de manière à être afocale ? (tu peux répondre en utilisant les points déjà portés sur le schéma)

c'est trés gentil d'avoir répondu!
mais le probeme c'est que moi aussi je n'est pas fait d'optique avec les lunette astronomique et donc je suis désolée de te dire ça mais je ne comprend pas trés bien ton shema je suis vraiment désolée ..

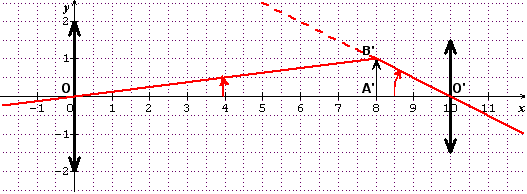
La double flèche de gauche est la représentation de l'objectif. Son centre optique est O

La double flèche de droite est la représentation de l'oculaire. Son centre optique est O'

L'axe optique relie les centres O et O' : on peut considérer que c'est aussi le trajet d'un rayon non dévié.

Passe par le point O un rayon rouge, qui n'est pas dévié (c'est une propriété du centre optique d'une lentille mince). Il parvient au point B' qui est l'image du point B (à l'infini à gauche).
Le point A' sur l'axe optique est l'image du point A (également à l'infini à gauche).

A'B' est donc l'image intermédiaire donnée par l'objectif de la lunette d'un objet AB (ici le rayon de la Lune) qui se trouve "à l'infini" à gauche.

Cette image intermédiaire A'B' est observée, comme avec une loupe, par l'oculaire. L'image A''B'' est à l'infini (également à gauche) si la lunette est afocale.

Mais si tu n'as pas fait d'optique... il te sera difficile de faire cet exercice.

en fait je croi que j'ai compris pourquoi je ne comprenais pas  c'est parceque tu as représenté que 1 rayon alors que d'habitude il y en a au moins trois qui sont représenté ...
donc voila mais ça veut pas dire que j'ai compris maitenant ... merci pour ta réponse !

C'est vrai... j'ai représenté pour chaque lentille un seul rayon de construction du point B' puis du point à l'infini B'' : mais cela suffit pour faire le problème !

Si tu veux un schéma avec beaucoup de rayons... et de quoi bien travailler sur la lunette astronomique, je te conseille d'aller explorer ce "laboratoire virtuel" :

Bonjour à tous
Pour la dernière question de l'exercice soit la question 4 b) mon résultat obtenu est 1.8*10^-5 rad je désirerai avoir une confirmation pour ce résultat s'il s'avère faux je posterai alors ma formule afin de comprendre mon erreur     .                                                                 Dors et déjà merci à ceux qui me répondront

Bonjour,

Je ne peux confirmer ce résultat.
Il n'y a même pas besoin de calculer pour savoir que ce résultat ne peut être que faux.
Une lunette astronomique est faite pour que l'image soit plus "grosse" que l'objet. C'est-à-dire pour que le rayon de la Lune, ici, soit vu sous un angle supérieur avec la lunette que celui sous lequel il est vu à l'œil nu.
A l'œil nu, cet angle vaut 4,4.10^-3 rad
Avec la lunette il doit être supérieur et en aucun cas inférieur (à moins de regarder par le mauvais bout... )